Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вероятность
|
|
Предположим, имеется некоторый эксперимент, где Ω — множество его возможных исходов; А — некоторое случайное событие, например бросание игральной кости; А = {появление четного числа}.
Повторим n раз эксперимент и подсчитаем количество 
(частоту) появлений события A. Обозначим 
относительную частоту появления А.
Проделаем эксперимент много раз. Относительная частота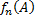 
с ростом n стабилизируется, частота 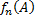стремится к некоторому предельному значению, обозначим его Р(А). Если мы зафиксируем другое случайное событие В, например В = {появление «6»}, то мы снова заметим, что частота 
стабилизируется, но стремится к другому значению — обозначим его Р(В). Эти наблюдения говорят нам о том, что каждому случайному событию объективно соответствует некоторое число — предел, к которому стремится относительная частота. Этот предел назовем вероятностью (точнее, статистической вероятностью).
Итак, неформально, физически (точнее, статистически), вероятность есть объективная характеристика случайного события, дающая представление о том, как часто появится событие при многократном повторении опыта.
Итак, статистическая вероятность — это предел для относительной частоты 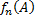. Очевидны свойства статистической вероятности:
1) Р(А)≥ 0;
2) P(Ω)=1;
3) если А и В несовместны, т.е.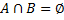 
, то Р(А+В) = Р(А)+Р(В), это следует из соотношения несовместности 
после деления на n и перехода к пределу.
В математической теории вероятность вводится следующим образом.
Аксиоматическое определение: числовая функция Р(А), введенная на подмножествах из Ω и удовлетворяющая свойствам 1, 2, 3, называется вероятностью.
При таком подходе соотношения 1, 2, 3 являются аксиомами вероятности, аксиома 3 называется аксиомой сложения. Дополнительно предполагается, что аксиома 3 верна для счетного числа несовместных событий:
3а) расширенная аксиома сложения. Если 
, то
.
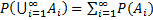Замечание. Механическим аналогом вероятности случайного события является вес соответствующего множества элементов, численно равный вероятности, причем вес Ω равен 1. Очевидно, аксиомы 1, 2 и 3 для веса выполняются.