
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Независимость случайных событий
|
|
Определение: Событие А независимо по отношению к событию В, если 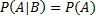
Следствие:
1. Если А независимо относительно В, то В независимо относительно А 
 . Т.е. свойство независимости взаимно.
. Т.е. свойство независимости взаимно.
2. Если А и В независимы, то
2.1  независимы (
независимы ( )
)
2.2  независимы (аналогично)
независимы (аналогично)
2.3 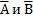 независимы (аналогично)
независимы (аналогично)
3. Если А и В независимы, то 
 ;
;
Определение: 1б: Случайные события А и В называются независимыми, если  (3*)
(3*)
Замечание: Случайные события А и В физически независимы, след. (3) выполняется и тогда (3*) используется для определения вероятности двух событий, т.е. Р(АВ)
Пример: Бросание 2-х монет
Случайное событие А={появление герба на 1-ой монете} Р(А)=1/2
Случайное событие В={появление герба на 2-ой монете} Р(В)=1/2
 ;
;
Определение 2: Случайные события  называются независимыми в совокупности, если
называются независимыми в совокупности, если 
Определение 3: Случайные события  называются попарно зависимыми, если
называются попарно зависимыми, если 
Из независимости совокупностей следует независимость попарно. Но обратное неверно.
Пример. 4 карты, на которых написаны числа 2, 3, 5, 30.
Извлекается 1 карточка
A1={результат делится на 2}; A2={результат делится на 3}; A3={результат делится на 5};
P(A1A2)=P(A1)*P(A2)=1/4=1/2*1/2; P(A1A3)=P(A1)*P(A3)=1/4=1/2*1/2; P(A2A3)=P(A2)*P(A3)=1/4=1/2*1/2;
Но: P(A1A2 A3)=P(A1)*P(A2)*P(A3)=1/4 