Независимость случайных величин. Условные распределения.

Независимость случайных величин

Напомним, что события А и В называются независимыми, если

Определение 1. Дискретные случайные величины и называются независимыми, если при любых и

или

Определение 2. Непрерывные случайные величины называются неза­висимыми, если для любых х и у для плотностей справедливо равенство:

Определение 3. Понятие независимости для случайных величин об­щего типа формулируется в терминах функций распределения. Величины и независимы, если

Определение 4. n случайных величин называются неза­висимыми в совокупности, если

Условные распределения

а) Рассмотрим сначала дискретные случайные величины 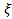и , опре­деляемые совокупностью точек на плоскости и соответствую­щими вероятностями . Предположим, что эксперимент прове­ден. Стало известно значение одной компоненты = у, но значение дру­гой компоненты остается неизвестным. Возникает вопрос: како­вы вероятности того, что имеет различные значения ? Выпишем эти вероятности по формуле условной вероятности:

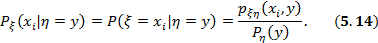
В этом выражении изменяется, а у зафиксирован.

Определение. Совокупность по вероятностей (5.14) называется условным распределением случайной величины при условии известного значения = у.

Просуммировав (5.14) по , с учетом (5.3б) убеждаемся, что

б) Рассмотрим непрерывные случайные величины и , определяе­мые плотностью совместного распределения . Предположим, что эксперимент проведен. Стало известно значение одной компоненты = у но значение другой () остается неизвестным. Каково теперь рас­пределение значений для

Определение. Плотностью условного распределения случайной вели­чины при условии известного значения = у называется функция от х:

Убедимся в том, что предел равен отношению плотностей. Действи­тельно

при . В выражении для условной плотности 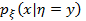переменной является х, а значение у фиксировано. Интегрирование (5.16) по х с учетом (5.3а) дает 1:

Замечания.

1. Поскольку значение у зафиксировано,

Эта запись означает, что условная плотность, как функция х, совпада­ет с точностью до константы с сечением функции двух переменных при фиксированном значении другой переменной. Нормирующая константа определяется из условия

2. Если 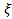и независимы, т.е. , то

т.е. условное распределение совпадает с безусловным.

3. Аналогично (5.16) вводится условное распределение случайной ве­личины при условии известного значения :

Замечания 1, 2, 3, сделанные для непрерывных случайных величин, справедливы и для дискретных, надо лишь плотности заменить вероятно­стями и интеграл — суммой.

Условные математические ожидания и условные дисперсии

Для условных распределений мы можем определить математическое ожидание, дисперсию и другие числовые характеристики. Они нужны для многих целей, в частности, для прогноза. Если стало известно значе­ние одной компоненты = у, и мы хотим предсказать ненаблюдаемую компоненту , то лучшим прогнозом является условное матема­тическое ожидание:

Например, известна на сегодня температура в Москве, а мы хотим предсказать температуру в Ярославле. Лучшим прогнозом является ус­ловное математическое ожидание. Здесь лучшим прогнозом мы понимаем такой, для которого средний квадрат ошибки минимален.

Для того чтобы рассматривать одновременно дискретные и непре­рывные случайные величины, будем использовать единое обозначение , понимая его как плотность, если и непрерывны, и как веро­ятность при дискретных аргументах, если и дискретны. Аналогично: условные распределения и распределения компо­нент .

Определение. Условным математическим ожиданием случайной ве­личины при условии известного значения = у называется

Определение. Условной дисперсией случайной ве­личины при условии известного значения = у называется

Поскольку значение у случайно, мы можем рассматривать значения функций и как случайные величины:

Справедливы следующие замечательные формулы:

Покажем справедливость (5.21) для дискретных случайных величин. Запишем формулу полной вероятности в наших обозначениях

Умножим это соотношение на х и просуммируем:

что означает

Покажем справедливость (5.22). По формуле (4.14), справедливой для любых распределений, в том числе условных

Здесь слева и справа — функции от у, которые мы можем рассматри­вать как функции от случайной величины :

Если определить математическое ожидание слева и справа (используя свойство из раздела 6: математическое ожидание суммы равно сумме математических ожиданий), то получим

Определим второе слагаемое в (5.22):

Складывая (5.23) и (5.24) и дважды применяя (5.21), получим (5.22):