Свойства дисперсии. Примеры.

1. Дисперсия константы c равна 0.

2. Прибавление константы не изменяет дисперсию.

3. Константа из-под знака дисперсии выносится с квадратом.

4. Для дисперсии суммы случайных величин используются формулы:

а)Для независимых случайных величин дисперсия суммы равна сумме дисперсий.

б)Для произвольных случайных величин

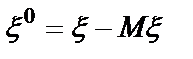, где и

5. Неравенство Чебышева: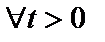

Это неравенство понимается так: вероятность большого отклонения слу­чайной величины от своего математического ожидания мала, и она тем меньше, чем меньше дисперсия.

Справедливость свойств (1-4) вытекает из определения дисперсии (1) и свойств математического ожидания. Действительно:

1)

2)

3)

4б)

4а)

Если события независимы то по:

5)доказательство д.б. в другом билете.

Пример 1 использования свойств. Проведем п независимых испыта­ний случайного события А, вероятность появления которого в одном ис­пытании Р(А) = р. Определим математическое ожидание и дисперсию количества успехов. Эту случайную величину можно представить сум­мой результатов п испытаний:

где

Согласно 4a и свойству суммы мат. ожиданий:

Пример 2. В устройстве n блоков. При испытании блок с номером i выходит из строя с вероятностью р_i. Определить среднее количество вы­ходящих из строя блоков, а также дисперсию.

Количество 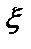выходящих из строя блоков можно представить в виде суммы по блокам:

где

19.Числовые характеристики многомерных случайных величин.

Пусть - многомерная случайная величина (вектор столбец).

Математическое ожидание — характеристика среднего значения случайной величины.

Определение. Математическим ожиданием , называется век­тор математических ожиданий:

(1)

Каждая компонента этого вектора может быть выражена через инте­грал:

Где функция распределения случайной величины ; F(x1, …, xn)- функция распределения случайной величины

Дисперсионная матрица — характеристика рассеяния

Определение. Дисперсионной (ковариационной) матрицей на­зывается матрица вторых центральных моментов:

где называется ковариацией случайных величин и . Если - непре­рывна и р(x1,.., х_n) — плотность вероятности, b_jk выражается очевид­ным образом через интеграл:

Дисперсионная матрица является симметричной:

В^Т = В

и неотрицательно определенной, т.е. для любых значений переменных t1, …, t_n

⁽¹⁾

Это свойство доказывается рассмотрением случайной величины - линейной комбинации :

Вычислим дисперсию . Поскольку = О

что совпадает с суммой в (1); но > 0, что и дает (1). Дисперсионную матрицу можно представить так: