Последовательность независимых испытаний Бернулли (биномиальный закон распределения)

Пусть имеется некоторый элементарный опыт. В результате опыта может произойти или не про­изойти некоторое событие А с вероятностью P(A)=p, P()=q=1-p.

Появление А будем считать " успехом", а непоявление А — «неуспе­хом». Повторим этот элементарный опыт n раз, в этом n - кратном по­вторении состоит основной эксперимент, который назовем независимы­ми испытаниями Бернулли. Введем случайную величину ξ — количество «успехов» в n испытаниях случайного события А. Ясно, что ξ может при­нимать значения 0, 1,..., n. Оказывается, вероятность получить k " успе­хов" равна

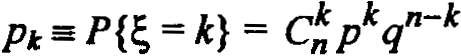(1)

Покажем справедливость этой формулы для n = 3 и k = 2. Для экспе­римента, состоящего из n = 3 испытаний, имеем 8 исходов: ω ₁=(0, 0, 0); ω ₂=(0, 0, 1); …; ω ₈=(1, 1, 1);

Событию {ξ = 2} благоприятствует 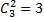исхода (1, 1, 0), (1, 0, 1) и (0, 1, 1), причем в силу независимости трех испытаний P(1, 1, 0)=P(1, 0, 1)=P(0, 1, 1)=p²q, и потому .

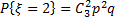Рассуждая аналогично, для произвольных n и k получим требуемую формулу.

Нетрудно видеть, что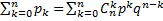

Действительно, это выражение совпадает с биномиальным разложением: .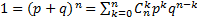

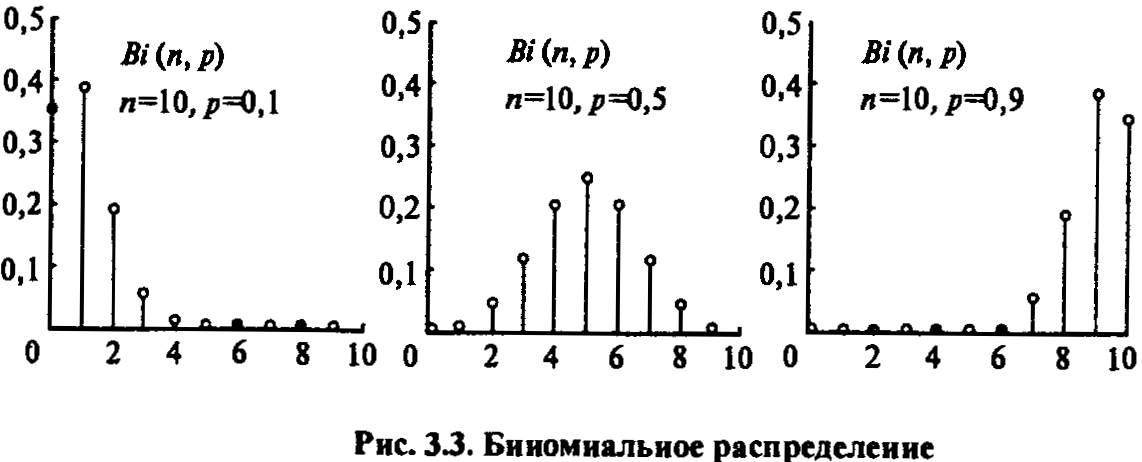
Совокупность {k, р_k}, определенных формулой (1), называется би­номиальным распределением вероятностей. Случайная величина ξ, для которой верно (1), обозначается: ξ ~ Bi(n, p) и читается так: случайная величина подчиняется биномиальному закону с парамет­рами n и p (n — число испытаний, р — вероятность " успеха" в одном испытании).

Типичная зависимость вероятности Р(k) от k показана на рис. 3.3.