Функции распределения и их свойства. Дискретные и непрерывные случайные величины.

10. Преобразование случайных величин. Примеры: линейное преобразование, логарифмически нормальное распределение.

11. Числовые характеристики случайных величин: математическое ожидание, дисперсия. Примеры: распределение Бернулли, Пуассона, нормальное, равномерное.

Пусть ξ – дискретная случайная величина, определяемая значениями x₁, x_2, …, x_k, … и соответствующими вероятностями p₁, p_2, …, p_k, …. Математическое ожидание Mξ определяется как сумма (1.1) (если ряд сходится абсолютно).
Пусть ξ – непрерывная случайная величина, определяемая плотностью p_ξ (x). Математическое ожидание Mξ определяется как интеграл 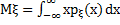(1.2) (если интеграл сходится абсолютно).
Замечание. Механическим аналогом математического ожидания является центр тяжести системы материальных точек. Пусть в точках x₁, x_2, …, x_k, … находятся материальные точки с массами m_k=p_k, равными вероятностями. Тогда центр тяжести x_ц этой системы есть , т.е. математической ожидание. Это позволяет иногда определять без вычислений.

Дисперсией случайной величины называется сумма (2), если дискретна и интеграл , если непрерывна. Справедлива формула , если дискретна (); .
Поскольку дисперсия получается усреднением квадрата единицы измерения случайной величины. Для того чтобы измерять разброс в исходных единицах, вводят понятие среднеквадратичного отклонения: .

Примеры: 1) Случайная величина, распределенная по биномиальному закону. . Поскольку ξ – это количество успехов в n испытаниях, ξ можно представить суммой результатов , где , т.е. ξ есть сумма независимых бинарных величин. Mξ и Dξ равны n-кратным значениям Mε _k и Dξ, т.е. Mξ =np; Dξ =npq.
2) Случайная величина, распределенная по закону Пуассона. ; k=0, 1, 2, … Согласно (1.1) . Согласно (2) . Затем . Итак, параметр a закона Пуассона имеет двойной вероятностный смысл: это математическое ожидание и одновременно дисперсия, причем стандартное отклонение
3) Случайная величина , распределенная по нормальному закону. Плотность распределения . Согласно (1.2) используя замену переменной , имеем , где первый интеграл равен 1, поскольку интегрируется плотность, а второй равен 0, поскольку под интегралом нечетная функция. С помощью той же замены нетрудно показать, что .
4) Случайная величина, распределенная по равномерному закону.

/*На основе формул математического ожидания и дисперсии получим*/ ;