Преобразование многомерных случайных величин. Распределение суммы двух случайных величин.

17.Свойства математического ожидания. Примеры.

1. Математическое ожидание константы есть константа:

(1)

2. Константа выносится за знак математического ожидания:

(2)

3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий:

(3)

4. Если случайные величины независимы, то математическое ожида­ние их произведения равно произведению математических ожиданий:

(4)

Покажем справедливость этих свойств.

1. Константу с можно рассматривать как вырожденную случайную величину, которая принимает единственное значение с с вероятностью 1.

2. Формула (2) доказывается применением формулы: (5), если положить

и с вынести за знак интеграла.

3. Формула (3) также доказывается с помощью формулы, аналогичной (5). Для дискретных случайных величин

(6)

Если в качестве взять сумму 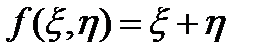, то по (6)

4. Аналогично показывается справедливость (4); для дискретных случайных величин, если они независимы, т.е. , имеем

Пример 1 использования свойств. Проведем п независимых испыта­ний случайного события А, вероятность появления которого в одном ис­пытании Р(А) = р. Определим математическое ожидание и дисперсию количества успехов. Эту случайную величину можно представить сум­мой результатов п испытаний:

где

Согласно 4a и свойству суммы мат. ожиданий:

Пример 2. В устройстве n блоков. При испытании блок с номером i выходит из строя с вероятностью р_i. Определить среднее количество вы­ходящих из строя блоков, а также дисперсию.

Количество 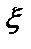выходящих из строя блоков можно представить в виде суммы по блокам:

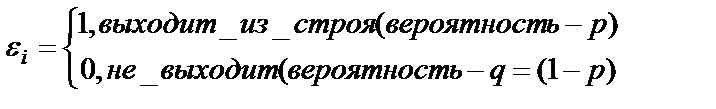
где