Одномерные случайные величины. Независимые испытания Бернулли.

Пусть имеется некоторый эксперимент, множество исходов Ω = {ω }, и на Ω задана вероятность Р(А), 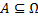. Исход ω - это элемент любой природы. Теперь будем полагать, что исход эксперимента - число.

Определение 1а. Случайной величиной называется числовой исход эксперимента.

Поскольку Ω — числовое множество, случайное событие определяет­ся множеством А точек на вещественной оси. Предполагается, что заданы вероятности Р{А) = Р{ }.

Случайные величины будем обозначать ξ, η, ζ, α, β и т.д. в отличие от ω - элемента произвольной природы.

Обобщим понятие случайной величины. Пусть {Ω, S, Р_Ω } — вероят­ностное пространство, Ω = {ω } — множество элементов произвольной природы.

Определение 16. Вещественнозначная функция ξ =f(ω), заданная на вероятностном пространстве, называется случайной величиной.

При таком введении случайной величины вероятность события Р{ }, где , определяется следующим образом: Ω содержит множество С_А тех исходов ω, для которых :

С_А={ω: }. Тогда

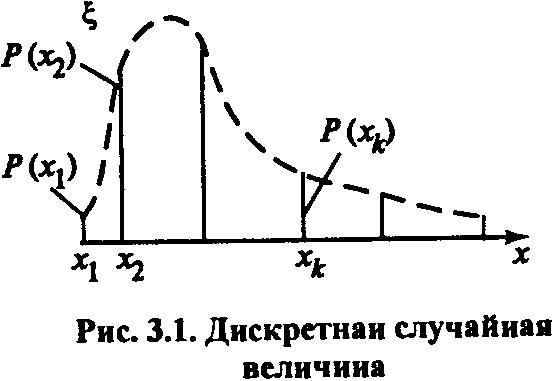Определение 2. Случайная величина называется дискретной, если множество ее значений конечно или счетно.Такую случайную вели­чинуможно задать множеством значений x₁, x₂. …, x_k, … и соответствующими вероятностями:

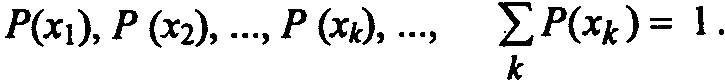
Дискретную случайную величину можно представить графически (рис. 3.1). Вероятность любого события Р{ }, , определяется очевидным образом:

т.е. суммируются вероятности тех х_k, которые находятся в А.