Задача №4. Трое рабочих цеха обслуживают станки

Трое рабочих цеха обслуживают станки. Первый рабочий обслуживает 20 станков, второй – 30 станков, третий – 50 станков. Вероятность того, что станки, обслуживаемые первым рабочим, в течение смены безотказно работают, равна 0, 9, для второго и третьего рабочих эта вероятность равна соответственно 0, 8 и 0, 7. А) Какова вероятность того, что выбранный наудачу станок цеха безотказно проработает в течение смены? Б) Станок цеха, выбранный наудачу, безотказно проработал в течение смены. Какова вероятность того, что этот станок обслуживается вторым рабочим?

Решение. Обозначим события: А – «выбранный наудачу станок цеха безотказно проработает в течение смены», гипотезы H_i – «станок обслуживается i -ым рабочим» (i =1, 2, 3). Вероятности гипотез находим по классическому определению вероятности:

, , ;

условие выполняется.

а) Вероятность того, чтовыбранный наудачу станок цеха безотказно проработает в течение смены, находим по формуле полной вероятности:

= 0, 77.

б) Если станок цеха, выбранный наудачу, безотказно проработал в течение смены, то вероятность того, что этот станок обслуживается вторым рабочим, найдем по формуле Байеса: .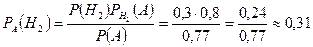

Ответ: А) Р= 0, 77; Б) Р = 0, 31.