Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приложения. Таблица значений локальной функции Лапласа x 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,0
|
|
Приложение № 1
Таблица значений локальной функции Лапласа 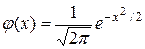
| x | 0, 00 | 0, 01 | 0, 02 | 0, 03 | 0, 04 | 0, 05 | 0, 06 | 0, 07 | 0, 08 | 0, 09 |
| 0, 0 | 0, 3989 | 0, 3989 | 0, 3989 | 0, 3988 | 0, 3986 | 0, 3984 | 0, 3982 | 0, 3980 | 0, 3977 | 0, 3973 |
| 0, 1 | 0, 3970 | 0, 3965 | 0, 3961 | 0, 3956 | 0, 3951 | 0, 3945 | 0, 3939 | 0, 3932 | 0, 3925 | 0, 3918 |
| 0, 2 | 0, 3910 | 0, 3902 | 0, 3894 | 0, 6885 | 0, 3876 | 0, 3867 | 0, 3857 | 0, 3847 | 0, 3836 | 0, 3825 |
| 0, 3 | 0, 3814 | 0, 3802 | 0, 3790 | 0, 3778 | 0, 3765 | 0, 3752 | 0, 3739 | 0, 3726 | 0, 3712 | 0, 3697 |
| 0, 4 | 0, 3683 | 0, 3668 | 0, 3652 | 0, 3637 | 0, 3621 | 0, 3605 | 0, 3589 | 0, 3572 | 0, 3555 | 0, 3538 |
| 0, 5 | 0, 3521 | 0, 3503 | 0, 3485 | 0, 3467 | 0, 3448 | 0, 3429 | 0, 3410 | 0, 3991 | 0, 3372 | 0, 3352 |
| 0, 6 | 0, 3332 | 0, 3312 | 0, 3292 | 0, 3271 | 0, 3251 | 0, 3230 | 0, 3209 | 0, 3187 | 0, 3166 | 0, 3144 |
| 0, 7 | 0, 3123 | 0, 3101 | 0, 3079 | 0, 3056 | 0, 3134 | 0, 3011 | 0, 2989 | 0, 2966 | 0, 2943 | 0, 2920 |
| 0, 8 | 0, 2897 | 0, 2874 | 0, 2850 | 0, 2827 | 0, 2803 | 0, 2780 | 0, 2756 | 0, 2732 | 0, 2709 | 0, 2685 |
| 0, 9 | 0, 2661 | 0, 2637 | 0, 2613 | 0, 2589 | 0, 2565 | 0, 2541 | 0, 2516 | 0, 2492 | 0, 2568 | 0, 2444 |
| 1, 0 | 0, 2420 | 0, 2396 | 0, 2371 | 0, 2347 | 0, 2323 | 0, 2299 | 0, 2275 | 0, 2227 | 0, 2203 | |
| 1, 1 | 0, 2179 | 0, 2155 | 0, 2131 | 0, 2107 | 0, 2083 | 0, 2059 | 0, 2036 | 0, 2012 | 0, 1989 | 0, 1965 |
| 1, 2 | 0, 1942 | 0, 1919 | 0, 1895 | 0, 1872 | 0, 1849 | 0, 1826 | 0, 1804 | 0, 1781 | 0, 1758 | 0, 1736 |
| 1, 3 | 0, 1714 | 0, 1691 | 0, 1669 | 0, 1647 | 0, 1626 | 0, 1604 | 0, 1582 | 0, 1561 | 0, 1539 | 0, 1518 |
| 1, 4 | 0, 1497 | 0, 1476 | 0, 1456 | 0, 1435 | 0, 1415 | 0, 1394 | 0, 1374 | 0, 1354 | 0, 1334 | 0, 1315 |
| 1, 5 | 0, 1295 | 0, 1276 | 0, 1257 | 0, 1238 | 0, 1219 | 0, 1200 | 0, 1182 | 0, 1163 | 0, 1145 | 0, 1127 |
| 1, 6 | 0, 1109 | 0, 1092 | 0, 1074 | 0, 1057 | 0, 1040 | 0, 1023 | 0, 1006 | 0, 0989 | 0, 0973 | 0, 0957 |
| 1, 7 | 0, 0940 | 0, 0925 | 0, 0909 | 0, 0893 | 0, 0878 | 0, 0863 | 0, 0848 | 0, 0833 | 0, 0818 | 0, 0804 |
| 1, 8 | 0, 0790 | 0, 0775 | 0, 0761 | 0, 0748 | 0, 0734 | 0, 0721 | 0, 0707 | 0, 0694 | 0, 0681 | 0, 0669 |
| 1, 9 | 0, 0656 | 0, 0644 | 0, 0632 | 0, 0620 | 0, 0608 | 0, 0596 | 0, 0584 | 0, 0573 | 0, 0562 | 0, 0551 |
| 2, 0 | 0, 0540 | 0, 0529 | 0, 0519 | 0, 0508 | 0, 0498 | 0, 0488 | 0, 0478 | 0, 0468 | 0, 0459 | 0, 0449 |
| 2, 1 | 0, 0440 | 0, 0431 | 0, 0422 | 0, 0413 | 0, 0404 | 0, 0396 | 0, 0387 | 0, 0379 | 0, 0371 | 0, 0363 |
| 2, 2 | 0, 0355 | 0, 0347 | 0, 0339 | 0, 0332 | 0, 0325 | 0, 0317 | 0, 0310 | 0, 0303 | 0, 0297 | 0, 0290 |
| 2, 3 | 0, 0283 | 0, 0277 | 0, 0270 | 0, 0264 | 0, 0258 | 0, 0252 | 0, 0246 | 0, 0241 | 0, 0235 | 0, 0229 |
| 2, 4 | 0, 0224 | 0, 0219 | 0, 0213 | 0, 0208 | 0, 0203 | 0, 0198 | 0, 0193 | 0, 0189 | 0, 0184 | 0, 0180 |
| 2, 5 | 0, 0175 | 0, 0171 | 0, 0167 | 0, 0163 | 0, 0158 | 0, 0154 | 0, 0151 | 0, 0147 | 0, 0143 | 0, 0139 |
| 2, 6 | 0, 0136 | 0, 0132 | 0, 0129 | 0, 0126 | 0, 0122 | 0, 0119 | 0, 0116 | 0, 0113 | 0, 0110 | 0, 0107 |
| 2, 7 | 0, 0104 | 0, 0101 | 0, 0099 | 0, 0096 | 0, 0093 | 0, 0091 | 0, 0088 | 0, 0086 | 0, 0084 | 0, 0081 |
| 2, 8 | 0, 0079 | 0, 0077 | 0, 0075 | 0, 0073 | 0, 0071 | 0, 0069 | 0, 0067 | 0, 0065 | 0, 0063 | 0, 0061 |
| 2, 9 | 0, 0060 | 0, 0058 | 0, 0056 | 0, 0055 | 0, 0053 | 0, 0051 | 0, 0050 | 0, 0048 | 0, 0047 | 0, 0046 |
| 3, 0 | 0, 0044 | 0, 0043 | 0, 0042 | 0, 0040 | 0, 0039 | 0, 0038 | 0, 0037 | 0, 0036 | 0, 0035 | 0, 0034 |
| 3, 1 | 0, 0033 | 0, 0032 | 0, 0031 | 0, 0030 | 0, 0029 | 0, 0028 | 0, 0027 | 0, 0026 | 0, 0025 | 0, 0025 |
| 3, 2 | 0, 0024 | 0, 0023 | 0, 0022 | 0, 0022 | 0, 0021 | 0, 0020 | 0, 0020 | 0, 0019 | 0, 0018 | 0, 0018 |
| 3, 3 | 0, 0017 | 0, 0017 | 0, 0016 | 0, 0016 | 0, 0015 | 0, 0015 | 0, 0014 | 0, 0014 | 0, 0013 | 0, 0013 |
| 3, 4 | 0, 0012 | 0, 0012 | 0, 0012 | 0, 0011 | 0, 0011 | 0, 0010 | 0, 0010 | 0, 0010 | 0, 0009 | 0, 0009 |
| 3, 5 | 0, 0009 | 0, 0008 | 0, 0008 | 0, 0008 | 0, 0008 | 0, 0007 | 0, 0007 | 0, 0007 | 0, 0007 | 0, 0006 |
| 3, 6 | 0, 0006 | 0, 0006 | 0, 0006 | 0, 0005 | 0, 0005 | 0, 0005 | 0, 0005 | 0, 0005 | 0, 0005 | 0, 0004 |
| 3, 7 | 0, 0004 | 0, 0004 | 0, 0004 | 0, 0004 | 0, 0004 | 0, 0004 | 0, 0003 | 0, 0003 | 0, 0003 | 0, 0003 |
| 3, 8 | 0, 0003 | 0, 0003 | 0, 0003 | 0, 0003 | 0, 0003 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0002 |
| 3, 9 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0002 | 0, 0001 | 0, 0001 |
| 4, 0 | 0, 0001 | 0, 0001 | 0, 0001 | 0, 0001 | 0, 0001 | 0, 0001 | 0, 0001 | 0, 0001 | 0, 0001 | 0, 0001 |
Приложение № 2
Таблица значений интегральной функции Лапласа 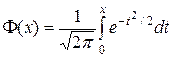
| x | F(x) | x | F(x) | x | F(x) | x | F(x) | x | F(x) |
| 0, 00 | 0, 0000 | 0, 52 | 0, 1985 | 1, 04 | 0, 3508 | 1, 56 | 0, 4406 | 2, 16 | 0, 4846 |
| 0, 01 | 0, 0040 | 0, 53 | 0, 2019 | 1, 05 | 0, 3531 | 1, 57 | 0, 4418 | 2, 18 | 0, 4854 |
| 0, 02 | 0, 0080 | 0, 54 | 0, 2054 | 1, 06 | 0, 3554 | 1, 58 | 0, 4429 | 2, 20 | 0, 4861 |
| 0, 03 | 0, 0120 | 0, 55 | 0, 2088 | 1, 07 | 0, 3577 | 1, 59 | 0, 4441 | 2, 22 | 0, 4868 |
| 0, 04 | 0, 0160 | 0, 56 | 0, 2123 | 1, 08 | 0, 3599 | 1, 60 | 0, 4452 | 2, 24 | 0, 4875 |
| 0, 05 | 0, 0199 | 0, 57 | 0, 2157 | 1, 09 | 0, 3621 | 1, 61 | 0, 4463 | 2, 26 | 0, 4881 |
| 0, 06 | 0, 0239 | 0, 58 | 0, 2190 | 1, 10 | 0, 3643 | 1, 62 | 0, 4474 | 2, 28 | 0, 4887 |
| 0, 07 | 0, 0279 | 0, 59 | 0, 2224 | 1, 11 | 0, 3665 | 1, 63 | 0, 4484 | 2, 30 | 0, 4893 |
| 0, 08 | 0, 0319 | 0, 60 | 0, 2257 | 1, 12 | 0, 3686 | 1, 64 | 0, 4495 | 2, 32 | 0, 4898 |
| 0, 09 | 0, 0359 | 0, 61 | 0, 2291 | 1, 13 | 0, 3708 | 1, 65 | 0, 4505 | 2, 34 | 0, 4904 |
| 0, 10 | 0, 0398 | 0, 62 | 0, 2324 | 1, 14 | 0, 3729 | 1, 66 | 0, 4515 | 2, 36 | 0, 4909 |
| 0, 11 | 0, 0438 | 0, 63 | 0, 2357 | 1, 15 | 0, 3749 | 1, 67 | 0, 4525 | 2, 38 | 0, 4913 |
| 0, 12 | 0, 0478 | 0, 64 | 0, 2389 | 1, 16 | 0, 3770 | 1, 68 | 0, 4535 | 2, 40 | 0, 4918 |
| 0, 13 | 0, 0517 | 0, 65 | 0, 2422 | 1, 17 | 0, 3790 | 1, 69 | 0, 4545 | 2, 42 | 0, 4922 |
| 0, 14 | 0, 0557 | 0, 66 | 0, 2454 | 1, 18 | 0, 3810 | 1, 70 | 0, 4554 | 2, 44 | 0, 4927 |
| 0, 15 | 0, 0596 | 0, 67 | 0, 2486 | 1, 19 | 0, 3830 | 1, 71 | 0, 4564 | 2, 46 | 0, 4931 |
| 0, 16 | 0, 0636 | 0, 68 | 0, 2517 | 1, 20 | 0, 3849 | 1, 72 | 0, 4573 | 2, 48 | 0, 4934 |
| 0, 17 | 0, 0675 | 0, 69 | 0, 2549 | 1, 21 | 0, 3869 | 1, 73 | 0, 4582 | 2, 50 | 0, 4938 |
| 0, 18 | 0, 0714 | 0, 70 | 0, 2580 | 1, 22 | 0, 3883 | 1, 74 | 0, 4591 | 2, 52 | 0, 4941 |
| 0, 19 | 0, 0753 | 0, 71 | 0, 2611 | 1, 23 | 0, 3907 | 1, 75 | 0, 4599 | 2, 54 | 0, 4945 |
| 0, 20 | 0, 0793 | 0, 72 | 0, 2642 | 1, 24 | 0, 3925 | 1, 76 | 0, 4608 | 2, 56 | 0, 4948 |
| 0, 21 | 0, 0832 | 0, 73 | 0, 2673 | 1, 25 | 0, 3944 | 1, 77 | 0, 4616 | 2, 58 | 0, 4951 |
| 0, 22 | 0, 0871 | 0, 74 | 0, 2703 | 1, 26 | 0, 3962 | 1, 78 | 0, 4625 | 2, 60 | 0, 4953 |
| 0, 23 | 0, 0910 | 0, 75 | 0, 2734 | 1, 27 | 0, 3980 | 1, 79 | 0, 4633 | 2, 62 | 0, 4956 |
| 0, 24 | 0, 0948 | 0, 76 | 0, 2764 | 1, 28 | 0, 3997 | 1, 80 | 0, 4641 | 2, 64 | 0, 4959 |
| 0, 25 | 0, 0987 | 0, 77 | 0, 2794 | 1, 29 | 0, 4015 | 1, 81 | 0, 4649 | 2, 66 | 0, 4961 |
| 0, 26 | 0, 1026 | 0, 78 | 0, 2823 | 1, 30 | 0, 4032 | 1, 82 | 0, 4656 | 2, 68 | 0, 4963 |
| 0, 27 | 0, 1064 | 0, 79 | 0, 2852 | 1, 31 | 0, 4049 | 1, 83 | 0, 4664 | 2, 70 | 0, 4965 |
| 0, 28 | 0, 1103 | 0, 80 | 0, 2881 | 1, 32 | 0, 4066 | 1, 84 | 0, 4671 | 2, 72 | 0, 4967 |
| 0, 29 | 0, 1141 | 0, 81 | 0, 2910 | 1, 33 | 0, 4082 | 1, 85 | 0, 4678 | 2, 74 | 0, 4969 |
| 0, 30 | 0, 1179 | 0, 82 | 0, 2939 | 1, 34 | 0, 4099 | 1, 86 | 0, 4686 | 2, 76 | 0, 4971 |
| 0, 31 | 0, 1217 | 0, 83 | 0, 2967 | 1, 35 | 0, 4115 | 1, 87 | 0, 4693 | 2, 78 | 0, 4973 |
| 0, 32 | 0, 1255 | 0, 84 | 0, 2995 | 1, 36 | 0, 4131 | 1, 88 | 0, 4699 | 2, 80 | 0, 4974 |
| 0, 33 | 0, 1293 | 0, 85 | 0, 3023 | 1, 37 | 0, 4147 | 1, 89 | 0, 4706 | 2, 82 | 0, 4976 |
| 0, 34 | 0, 1331 | 0, 86 | 0, 3051 | 1, 38 | 0, 4162 | 1, 90 | 0, 4713 | 2, 74 | 0, 4977 |
| 0, 35 | 0, 1368 | 0, 87 | 0, 3078 | 1, 39 | 0, 4177 | 1, 91 | 0, 4719 | 2, 86 | 0, 4979 |
| 0, 36 | 0, 1406 | 0, 88 | 0, 3106 | 1, 40 | 0, 4192 | 1, 92 | 0, 4726 | 2, 88 | 0, 4980 |
| 0, 37 | 0, 1443 | 0, 89 | 0, 3133 | 1, 41 | 0, 4207 | 1, 93 | 0, 4732 | 2, 90 | 0, 4981 |
| 0, 38 | 0, 1480 | 0, 90 | 0, 3159 | 1, 42 | 0, 4222 | 1, 94 | 0, 4738 | 2, 92 | 0, 4982 |
| 0, 39 | 0, 1517 | 0, 91 | 0, 3186 | 1, 43 | 0, 4236 | 1, 95 | 0, 4744 | 2, 94 | 0, 4984 |
| 0, 40 | 0, 1554 | 0, 92 | 0, 3212 | 1, 44 | 0, 4251 | 1, 96 | 0, 4750 | 2, 96 | 0, 4985 |
| 0, 41 | 0, 1591 | 0, 93 | 0, 3238 | 1, 45 | 0, 4265 | 1, 97 | 0, 4756 | 2, 98 | 0, 4986 |
| 0, 42 | 0, 1628 | 0, 94 | 0, 3264 | 1, 46 | 0, 4279 | 1, 98 | 0, 4761 | 3, 00 | 0, 49865 |
| 0, 43 | 0, 1664 | 0, 95 | 0, 3289 | 1, 47 | 0, 4292 | 1, 99 | 0, 4767 | 3, 20 | 0, 49931 |
| 0, 44 | 0, 1700 | 0, 96 | 0, 3315 | 1, 48 | 0, 4306 | 2, 00 | 0, 4772 | 3, 40 | 0, 49966 |
| 0, 45 | 0, 1736 | 0, 97 | 0, 3340 | 1, 49 | 0, 4319 | 2, 02 | 0, 4783 | 3, 60 | 0, 499841 |
| 0, 46 | 0, 1772 | 0, 98 | 0, 3365 | 1, 50 | 0, 4332 | 2, 04 | 0, 4793 | 3, 80 | 0, 499928 |
| 0, 47 | 0, 1808 | 0, 99 | 0, 3389 | 1, 51 | 0, 4345 | 2, 06 | 0, 4803 | 4, 00 | 0, 499968 |
| 0, 48 | 0, 1844 | 1, 00 | 0, 3413 | 1, 52 | 0, 4357 | 2, 08 | 0, 4812 | 4, 50 | 0, 499997 |
| 0, 49 | 0, 1879 | 1, 01 | 0, 3438 | 1, 53 | 0, 4370 | 2, 10 | 0, 4821 | 5, 00 | 0, 499997 |
| 0, 50 | 0, 1915 | 1, 02 | 0, 3461 | 1, 54 | 0, 4382 | 2, 12 | 0, 4830 | ||
| 0, 51 | 0, 1950 | 1, 03 | 0, 3485 | 1, 55 | 0, 4394 | 2, 14 | 0, 4838 |
Приложение № 3
Справочные материалы по теории вероятностей
и математической статистике
1. Формулы комбинаторики.
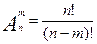 -размещения из n элементов по m элементов (порядок элементов важен);
-размещения из n элементов по m элементов (порядок элементов важен);
 - сочетания из n элементов по m элементов (порядок элементов не важен)
- сочетания из n элементов по m элементов (порядок элементов не важен)
 перестановки из m элементов (порядок элементов важен);
перестановки из m элементов (порядок элементов важен);
Частные случаи для вычисления сочетаний:
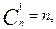


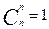
2. Классическая вероятность используется в случаях, когда число исходов конечно.
P (A) =  , где
, где
m - число исходов, благоприятствующих данному событию,
n - общее число несовместных равновозможных исходов события.
3. Условная вероятность (вероятность события Х при условии, что событие А произошло):
 .
.
Геометрически  ,
, 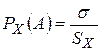 .
.
 4.Основные теоремы и формулы теории вероятностей
4.Основные теоремы и формулы теории вероятностей
Т.1.  , если А, В – независимые;
, если А, В – независимые;
Т.2.  , если А, В – зависимые.
, если А, В – зависимые.
Т.3. 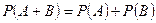 , если А, В – несовместные;
, если А, В – несовместные;
Т.4. 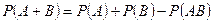 , если А, В – совместные.
, если А, В – совместные.
Т.5.  .
.
Следствие.  , N – невозможное, D – достоверное.
, N – невозможное, D – достоверное.
Т.6.  (формула полной вероятности),
(формула полной вероятности),
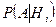 – вероятность события А при условии наступления Нi (i=1, 2, …, n).
– вероятность события А при условии наступления Нi (i=1, 2, …, n).
Т.7.  (формула Байеса).
(формула Байеса).
5. Повторение испытаний (повторяющиеся события).
Схема повторения испытаний:
1) проводится n независимых испытаний;
2) вероятность появления события А в каждом испытании  - const.
- const.
а) Формула Бернулли (вероятность k появлений события А в n испытаниях): 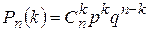 ,
, 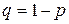 ,
,  - число сочетаний из n по k.
- число сочетаний из n по k.
Наивероятнейшее число появлений события А равно 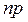
б) Формула Пуассона (n – велико, р - мало, 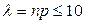 ):
):
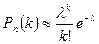 ,.
,.
в) Локальная теорема Лапласа:  ,
,  ;
;
применяется, если  велико, вероятность
велико, вероятность  не является маленькой.
не является маленькой.
г) Интегральная теорема Лапласа
 ,
, 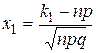 ,
, 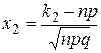 ;
;
 , где
, где  :
:  , где
, где 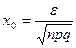
6. Дискретные случайные величины.
Закон распределения, или ряд распределения с.в. Х:

| 
| 
| 
| … | 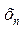
|
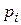
| 
| 
| 
| … | 
|
Математическое ожидание: 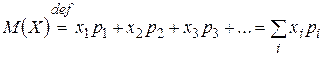 .
.
Дисперсия:  =
= 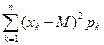 =
= 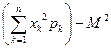
Среднее квадратическое отклонение:  .
.
Интегральная функция распределения:  .
.
Вероятность того, что с.в. Х принимает значения в интервале  :
:
 .
.
7. Непрерывные случайные величины (НСВ).
а) Интегральная функция распределения 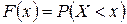
Свойства:
1) Функция распределения НСВ. Х есть непрерывная функция,
2)  ,
,  ,
,
3)  возрастающая функция.
возрастающая функция.
б) Дифференциальная функция распределения (плотность распределения):
 или
или  .
.
Свойства: 1)  ;
;
2)  (нормированность).
(нормированность).
в) Основные соотношения:
Вероятность попадания НСВ Х в интервал  :
:
 =
=  .
.
Вероятность попадания НСВ Х в точку равна 0.
Функция распределения 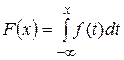 .
.
Математическое ожидание НСВ  .
.
Дисперсия: 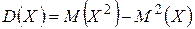 ,
,  .
.
г) Мода непрерывной случайной величины – то значение х, в котором плотность распределения вероятностей  достигает максимума.
достигает максимума.
Если случайная величина имеет одну моду, то она называется унимодальной, в противном случае – полимодальным.
Медиана случайной величины – значение  , для которого
, для которого
 ,
,  .
.
Медиана непрерывной случайной величины определяется равенством
 .
.
Если график плотности вероятностей  имеет ось симметрии
имеет ось симметрии  , то медиана
, то медиана  .
.
д) Начальным моментом k-го порядка 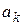 случайной величины Х называется математическое ожидание с.в.
случайной величины Х называется математическое ожидание с.в.  :
:  ;
;
 ,
,  .
.
Центральным моментом k-го порядка 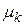 случайной величины Х называется математическое ожидание с.в.
случайной величины Х называется математическое ожидание с.в.  :
:  ;
;
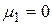 ,
,  .
.
е) Коэффициент асимметрии:  ,
,
где  – центральный момент третьего порядка,
– центральный момент третьего порядка, 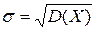 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Коэффициент эксцесса (эксцесс):  ,
,
где  ,
,  .
.
Коэффициенты асимметрии и эксцесса характеризуют степень отличия функции распределения  случайной величины Х от функции распределения
случайной величины Х от функции распределения  стандартного нормального распределения, для которого коэффициенты асимметрии и эксцесса равны нулю (a =0, e =0)
стандартного нормального распределения, для которого коэффициенты асимметрии и эксцесса равны нулю (a =0, e =0)
ж) Свойства математического ожидания и дисперсии
1. 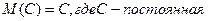
2. 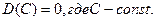
3.  :
:
4.  ,
,
5.  ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9.  , если Х и У независимы.
, если Х и У независимы.
з) Соотношения СВ
Если СВ имеет функцию распределения  , то случайная величина
, то случайная величина  имеет функцию распределения
имеет функцию распределения  , например, при
, например, при  имеем
имеем  и
и 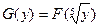
8. Распределение непрерывных случайных величин.
а) Равномерное распределение на отрезке.
 Если случайная величина может принимать значения только на отрезке
Если случайная величина может принимать значения только на отрезке  , причем попадания ее на все интервалы одинаковой длины равновероятны, то эта случайная величина имеет равномерное распределение
, причем попадания ее на все интервалы одинаковой длины равновероятны, то эта случайная величина имеет равномерное распределение
с плотностью  .
.
Функция распределения равномерной
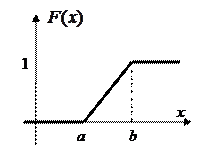 случайной величины
случайной величины  :
:  .
.
Числовые характеристики равномерного распределения:
 ,
,  ,
,  .
.
Коэффициент асимметрии a =0, эксцесс e =-1, 2.
Примеры равномерного распределения: ошибки при округлении отсчетов измерительных приборов до целых делений, время ожидания периодически происходящего явления.
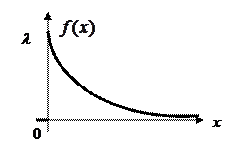 б) Показательное (экспоненциальное) распределение.
б) Показательное (экспоненциальное) распределение.
Плотность вероятностей показательного распределения:
 .
.
Функция распределения:
 .
.
Характеристики показательного распределения 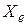 :
:
 ,
,  ,
,  .
.
Медиана 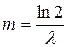 , коэффициент асимметрии a =2, эксцесс e =6.
, коэффициент асимметрии a =2, эксцесс e =6.
Примеры показательного распределения: время безотказной работы прибора, двигателя. Другие приложения показательного распределения – в физике, биологии, в теории массового обслуживания, в вопросах надежности.
г) Нормальное распределение (гауссовское распределение, лапласовское распределение, распределение Лапласа-Гаусса, второй закон Лапласа).
 Плотность нормального распределения:
Плотность нормального распределения:  ,
, 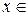 R.
R.
Параметры нормального распределения  :
:
 - математическое ожидание,
- математическое ожидание,
 = - дисперсия
= - дисперсия
 - среднее квадратическое отклонение,
- среднее квадратическое отклонение,
Мода и медиана нормального распределения совпадают с математическим ожиданием а. Коэффициенты асимметрии и эксцесса нормального распределения равны нулю (a =0, e =0).
Вероятность попадания нормальной с.в.  в интервал
в интервал 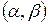 :
:
 ,
,
 .
.
При  получим «правило трех сигм»:
получим «правило трех сигм»:  , т.е. практически достоверно значения
, т.е. практически достоверно значения  принадлежат интервалу
принадлежат интервалу  ).
).
При  ,
,  получаем стандартное нормальное распределение
получаем стандартное нормальное распределение  : плотность
: плотность 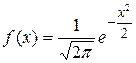 ,
,
Функция распределения: 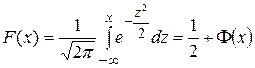 .
.
На рисунке приведено семейство кривых нормальных плотностей в зависимости от параметров а, σ. С геометрической точки зрения параметр а – точка максимума плотности и центр симметрии; σ определяет крутизну кривой и величину максимума.
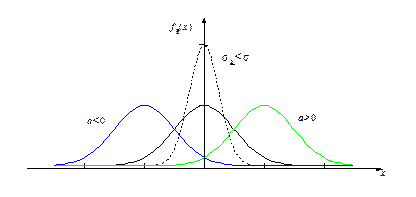
Семейство плотностей нормальных кривых
Нормальное распределение безгранично делимо: если сумма двух независимых случайных величин имеет нормальное распределение, то и каждая из этих случайных величин имеет нормальное распределение.
Особая роль нормального распределения определяется предельной теоремой Ляпунова, согласно которой (при не очень жестких ограничениях) сумма большого числа независимых случайных величин имеет распределение, близкое к нормальному, независимо от того, как распределены сами слагаемые.
9. Закон больших чисел и центральная предельная теорема
а) неравенство Маркова; 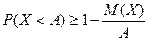 ,
, 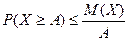
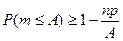
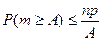
б) неравенство Чебышева; 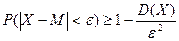 ,
, 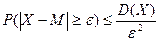
Пусть вероятность наступления события А в каждом из 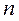 произведенных испытаний равна
произведенных испытаний равна  .
.
а) Вероятность того, что частота  наступления события А отличается от вероятности
наступления события А отличается от вероятности 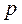 менее чем на
менее чем на  :
:  ,
,
Вероятность того, что частота  наступления события А отличается от вероятности
наступления события А отличается от вероятности 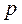 не менее чем на
не менее чем на  :
:  ,
,
б) Вероятность того, что число 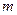 наступления события А отличается от математического ожидания
наступления события А отличается от математического ожидания 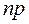 менее чем на
менее чем на  :
: 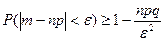
Вероятность того, что число 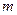 наступления события А отличается от математического ожидания
наступления события А отличается от математического ожидания 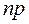 не менее чем на
не менее чем на  :
: