
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обозначения и дополнительные формулы для случая типической выборки
|
|
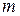 - число типических групп,
- число типических групп,
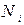 - численность
- численность 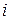 -ой группы в генеральной совокупности,
-ой группы в генеральной совокупности,
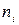 - число отобранных единиц из
- число отобранных единиц из 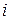 -ой группы,
-ой группы,
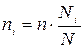 (при пропорциональном отборе),
(при пропорциональном отборе),
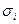 - выборочная дисперсия для
- выборочная дисперсия для 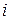 -ой группы (групповая выборочная дисперсия),
-ой группы (групповая выборочная дисперсия),
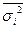 - средняя среди групповых в выборочных дисперсий,
- средняя среди групповых в выборочных дисперсий,
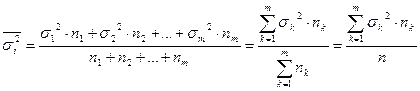 ,
,
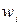 -выборочная доля для
-выборочная доля для 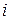 -ой группы,
-ой группы,
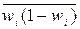 - средняя среди выборочных долей,
- средняя среди выборочных долей,
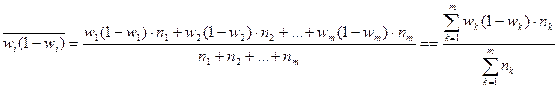
Обозначения и дополнительные формулы для серийной выборки.
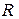 - общее число серий,
- общее число серий,
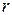 - число отобранных серий,
- число отобранных серий,
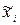 - средняя для
- средняя для 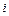 -ой серии,
-ой серии,
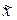 - средняя для всей выборочной совокупности,
- средняя для всей выборочной совокупности,
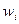 - доля признака для
- доля признака для 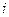 -ой серии,
-ой серии,
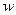 - доля признака для всей выборочной совокупности,
- доля признака для всей выборочной совокупности,
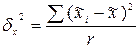 - межсерийная дисперсия признака,
- межсерийная дисперсия признака,
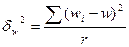 межсерийная дисперсия доли.
межсерийная дисперсия доли.
Формулы для определения необходимого объема выборки (n)
| метод отбора выборка | повторный | бесповторный | ||
| для средней (количественный признак) | для доли (альтернативный признак) | для средней (количественный признак) | для средней (альтернативный признак) | |
| Собственно-случайная. Механическая |
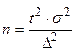
|
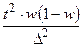
|
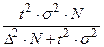
|
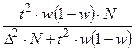
|
| Типическая (при пропорциональном отборе) |
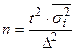
|
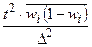
|
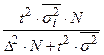
|
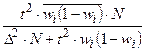
|
| Серийная |
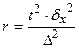
|
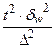
|
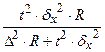
|
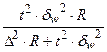
|
Коэффициент доверия 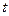 связан с вероятностью
связан с вероятностью 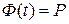
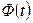 - функция Лапласа, ее значение определяется по таблицам.
- функция Лапласа, ее значение определяется по таблицам.
Репрезентативность результатов выборочного наблюдения зависит от: вариации признака и объема выборки.
Чтобы уменьшить ошибку выборки, рассчитанную в условиях повторного собственно-случайного отбора, можно увеличить численность выборочной совокупности или провести бесповторный отбор.
При малой выборке для расчета средней ошибки выборки используют формулу 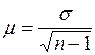 .
.
Ошибка наблюдения – это расхождение между расчетным и действительным значением изучаемых величин.
Систематическая ошибка репрезентативности - это отклонение выборочных характеристик от соответствующих характеристик генеральной совокупности, возникающее вследствие нарушения принципа случайности отбора.
Случайная ошибка репрезентативности – это отклонение выборочных характеристик от соответствующих характеристик генеральной совокупности, возникающее вследствие несплошного характера наблюдения.
Систематическая ошибка регистрации – это отклонение рассчитанных выборочных характеристик от соответствующих действительных характеристик выборочной совокупности, возникающее вследствие поступления искаженной информации от единиц совокупности.
Случайная ошибка регистрации – это отклонение рассчитанных выборочных характеристик от соответствующих действительных характеристик выборочной совокупности, возникающее вследствие действия случайных факторов.
Вариационные ряды
а) дискретный
| варианта | 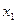
| 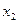
| 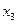
| … | 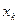
| Всего |
| частота | 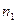
| 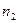
| 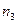
| … | 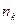
| 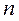
|
б) интервальный
| варианта | 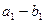
| 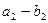
| 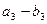
| … | 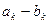
| Всего |
| частота | 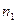
| 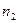
| 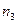
| … | 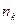
| 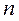
|
Относительная частота равна 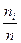
Среднее выборочное равно 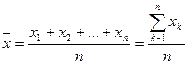 .
.
Дисперсия выборки равна 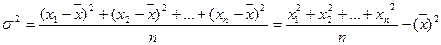
Если математическое ожидание оценки 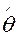 параметра
параметра 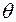 равно оцениваемому параметру, то оценка называется несмещенной
равно оцениваемому параметру, то оценка называется несмещенной
Если оценка 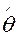 параметра
параметра 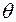 сходится по вероятности к оцениваемому параметру по вероятности при числе наблюдений
сходится по вероятности к оцениваемому параметру по вероятности при числе наблюдений 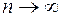 , то оценка называется состоятельной
, то оценка называется состоятельной
Несмещенная состоятельная оценка математического ожидания равна
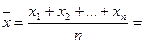
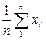
Несмещенная оценка дисперсии равна 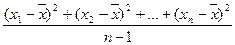
Смещенная оценка дисперсии равна
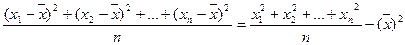
Несмещенная оценка среднего квадратического отклонения 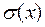 случайной величины X равна
случайной величины X равна 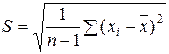
Если статистическая гипотеза Н однозначно определяет распределение случайной величины X, то она называется простой.
Если статистическая гипотеза Н определяет неоднозначно распределение случайной величины X, то она называется сложной.
Статистическая гипотеза — это любое предположение о параметрах известных распределений.
Гипотезы о значениях параметров распределения или о сравнительной величине параметров двух распределений называются параметрическими.
Гипотезы о виде распределения называются непараметрическими.
Проверить статистическую гипотезу - значит проверить, согласуются ли выборочные данные с выдвинутой гипотезой.
Ошибка первого рода состоит в том, что будет отвергнута верная гипотеза.
Ошибка второго рода состоит в том, что будет принята ложная гипотеза.
Уровень значимости – это вероятность совершения ошибки первого рода, то есть вероятность того, что будет отвергнута верная гипотеза.
Приложение 4
Некоторые часто встречающиеся постоянные
| Величина | Значение | Величина | Значение | |
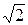
| 1, 4142 | е | 2, 7183 | |
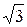
| 1, 7321 | 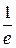 = e = e 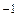
| 0, 3679 | |
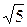
| 2, 2361 | 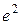
| 7, 3891 | |
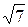
| 2, 6458 | 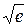
| 1, 6487 | |
| p | 3, 1416 | 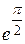
| 4, 8105 | |
| 2 p | 6, 2832 | 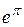
| 23, 1407 | |
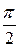
| 1, 5708 | 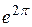
| 535, 4917 | |
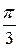
| 1, 0472 | 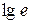
| 0, 4343 | |
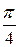
| 0, 7854 | 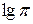
| 0, 4972 | |

| 0, 5236 | 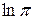
| 1, 1447 | |
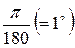
| 0, 0175 | 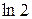
| 0, 6931 | |
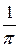
| 0, 3183 | 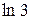
| 1, 0986 | |
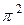
| 9, 8696 | 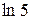
| 1, 6094 | |
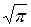
| 1, 7725 | 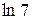
| 1, 9459 | |
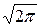
| 2, 5066 | e 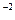
| 0, 1353 |
Глушкова Августа Игоревна