Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача №7. Вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,6
|
|
Вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0, 6. Предприятие закупило 3 телевизора. Требуется: а) найти закон распределения вероятностей дискретной случайной величины X – число телевизоров, потребующих ремонта в течение гарантийного срока; б) определить вид закона распределения вероятностей; в) построить многоугольник распределения; г) составить функцию распределения вероятностей случайной величины и построить ее график; д) вычислить числовые характеристики X; е) найти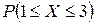 
.
Решение.
а) Составим закон распределения случайной величины X. Из трех купленных предприятием телевизоров могут потребовать ремонта в течение гарантийного срока три, два, один телевизор или, вообще, ни один из них может не потребовать ремонта. Поэтому получаем таблицу возможных значений X:
| xi | ||||
| pi | p 0 | p 1 | p 2 | p 3 |
Найдем вероятности pi (i =1, 2, 3, 4), используя формулу Бернулли. Если производится серия n независимых испытаний, при каждом из которых вероятность наступления события постоянна и равна p, тогда вероятность того, что это событие в n испытаниях появится ровно k раз, вычисляется по формуле:
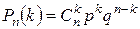, где 
и q =1- p.
Имеем: p =0, 6, q= 1 - 0, 6 = 0, 4, n= 3. Тогда:
;
;
;
.
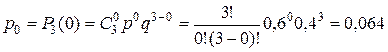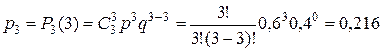Проверим тот факт, что 
. Действительно, 0, 064+0, 288+0, 432+ +0, 216=1. Следовательно, закон распределения X окончательно имеет вид:
| xi | ||||
| pi | 0, 064 | 0, 288 | 0, 432 | 0, 216 |
б) Поскольку при нахождении вероятностей pi была использована формула Бернулли, то указанная случайная величина имеет биномиальный закон распределения вероятностей.
в) Многоугольник распределения (рис. 3) – ломаная, звенья которой соединяют точки с координатами 
(i= 0, 1, 2, 3).
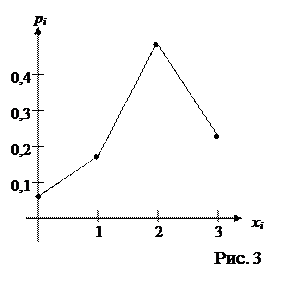
г) Функция распределения вероятностей случайной величины X определяется равенством F (x)= P (X < x). Имеем:
.
Построим график этой функции (рис. 4):
д) Найдем числовые характеристики X.
Математическое ожидание случайной величины X определяется равенством: 
. Имеем:
.
Для нахождения дисперсии составим закон распределения вероятностей случайной величины X 2:
| ||||
| pi | 0, 064 | 0, 288 | 0, 432 | 0, 216 |
Найдем математическое ожидание X 2:
.
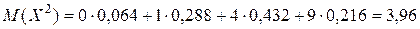Тогда, вычисляя дисперсию случайной величины X по формуле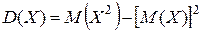 
, получаем: 
.
Среднее квадратическое отклонение случайной величины X находится как 
. Имеем: 
.
е) Для нахождения вероятности попадания случайной величины X в промежуток используем формулу: 
. Получаем: 
.