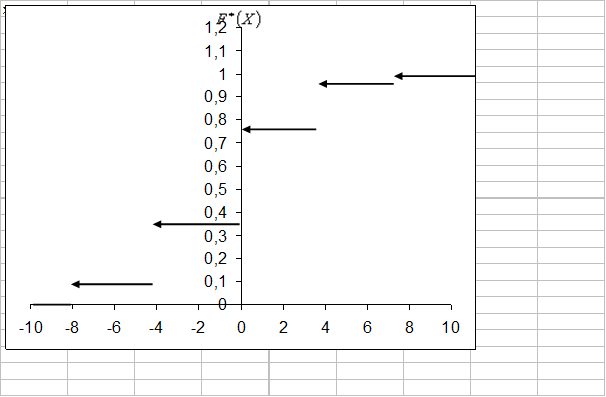Задача №9

Ошибки 1000 результатов измерений дальности приведены в таблице:

Построить гистограмму и эмпирическую функцию распределения ошибок измерения дальности.

Решение:

Объём выборки n = 1000

Длина каждого отдельного интервала h =4

1) Построим гистограмму /4 плотностей относительных частот.

Гистограммой называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны частотам или относительным частотам соответствующих интервалов или отношению /h, то есть плотности относительной частоты.

w = = n /n – относительная частота

Интервал (h)	(-10; -6)	(-6; -2)	(-2; 2)	(2; 6)	(6; 10)
Частота n
w = = n /n	0, 1	0, 26	0, 4	0, 2	0, 04
w /h= /4	0, 025	0, 065	0, 1	0, 05	0, 01

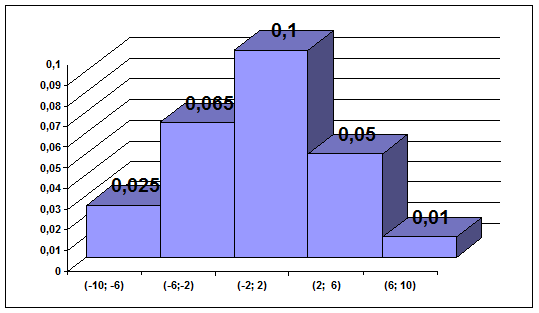
2) Интервальный ряд преобразуем в дискретный и найдём эмпирическую функцию распределения ошибок измерения дальности. Для преобразования в дискретный ряд в каждом интервале найдём середину каждого интервала – варианта Х.

Для нахождения эмпирической функции для каждого значения Х вычисляем накопленную относительную частоту.

Итак, функция распределения имеет вид:

0, при х -8

0, 1, при -8< х -4

0, 36, при -4 < х 0

= 0, 76, при 0 < х 4

0, 96, при 4 < х 8

1, при х > 8

Построим график функции :