Задача №8

Случайная величина X задана интегральной функцией распределения вероятностей . А) построить график функции F(x); б) найти дифференциальную функцию распределения вероятностей f(x) и построить ее график; в) вычислить числовые характеристики X; г) найти .

Решение.

а) Построим график интегральной функции распределения вероятностей (рис. 5).

б) Дифференциальную функцию распределения вероятностей определяем по формуле: . Имеем: .

Построим график этой функции (рис. 6).

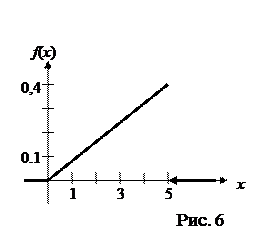
в) Вычислим числовые характеристики X.

Математическим ожиданием непрерывной случайной величины X называется значение интеграла , где f (x)– дифференциальная функция распределения вероятностей. В нашем случае

.

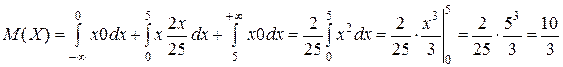Для нахождения дисперсии непрерывной случайной величины X может быть использована формула , где f (x)– дифференциальная функция распределения вероятностей. Получаем:

.

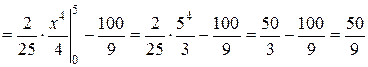Среднее квадратическое отклонение . Имеем: .

г) Для нахождения воспользуемся формулой . Тогда искомая вероятность 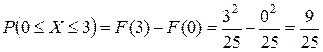.