
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Напряжения на наклонных площадках и условия на поверхности.
|
|
При решении различных задач требуется определить величину и направление компонент напряжений по площадкам, наклоненным к координатным осям, а также величину и направление компонент напряжений на поверхности тела. При этом, у поверхности выделить элементарный параллелепипед не представляется возможным.
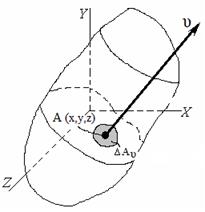
 Вокруг некоторой произвольной точки А (x, y, z), расположенной внутри тела, нагруженного внешними силами, выделена площадка ∆ А произвольной формы с нормалью.
Вокруг некоторой произвольной точки А (x, y, z), расположенной внутри тела, нагруженного внешними силами, выделена площадка ∆ А произвольной формы с нормалью.
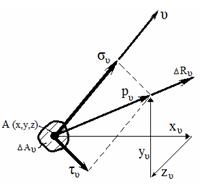
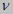
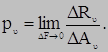
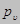 По элементарной площадке действует равнодействующая внутренних сил ∆ R
По элементарной площадке действует равнодействующая внутренних сил ∆ R
Полное напряжение
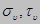 его составляющие:
его составляющие:
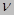
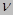
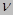 Проекции полного напряжения на координатные оси: x, y, z.
Проекции полного напряжения на координатные оси: x, y, z.
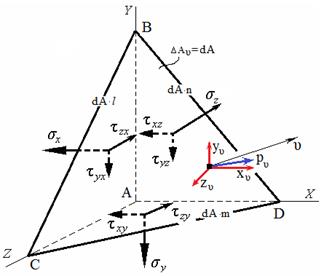
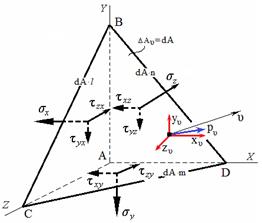
Рассечем параллелепипед наклонной плоскостью, пересекающей координатные оси в точках В, С, D.
Получили наклонную площадку ∆ Аυ , нормаль к которой υ.

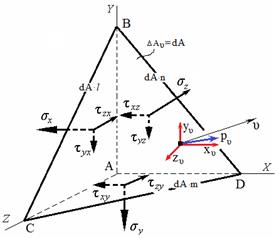
Положение наклонной площадки определяется углами (направляющими косинусами) между нормалью и соответствующими осям координат.
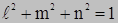 | |||
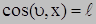 | |||
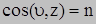 | |||
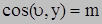 |
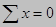 | 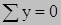 | 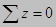 | |||
Уравнения равновесия
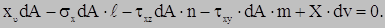 |
Произведением объемных сил пренебрегаем
(величина третьего порядка малости).
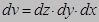 |
Уравнения, по которым определяются компоненты напряжений, действующих на произвольной поверхности с нормалью υ:
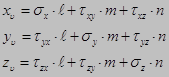 | |||||||
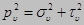 | 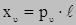 | 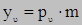 | 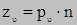 |
Условие на поверхности
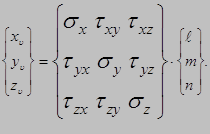 Запись условий на поверхности в матричной форме
Запись условий на поверхности в матричной форме
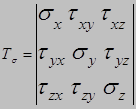 12. Тензор напряжений и его составляющие. Главные площадки и главные напряжения. Виды напряженных состояний.
12. Тензор напряжений и его составляющие. Главные площадки и главные напряжения. Виды напряженных состояний.
Матрицу напряжений называют тензором. Обозначают Тσ .
Тензор напряжений описывает напряженное состояние в точке.
Запишем среднее от суммы нормальных напряжений
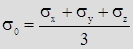
Среднее напряжение
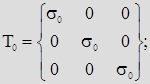
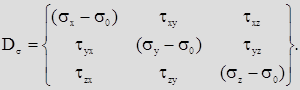 Тогда любое напряженное состояние, описываемое тензором напряжений Тσ , можно представить суммой двух НС:
Тогда любое напряженное состояние, описываемое тензором напряжений Тσ , можно представить суммой двух НС:
Шаровой тензор Т0 – характеризует НС, отвечающее всестороннему сжатию или растяжению, которое приводит только к изменению объема.
Девиатор Dσ – характеризует НС, приводящее только к изменению формы.
Главные напряжения и главные площадки
При изменении положения выделенного элемента (при его повороте в пространстве)
Теория упругости доказывает, что всегда можно найти такое положение элемента, при котором на его гранях касательные напряжения будут отсутствовать, т.е. равняться нулю.
Площадки, по которым не действуют касательные напряжения, называются главными площадками.
Экстремальные нормальные напряжения σ на этих площадках – г лавные напряжения.
В теории упругости также доказывается, что в каждой точке любым образом нагруженного тела всегда имеются
три главные взаимно перпендикулярныеплощадки.
Главные напряжения принято обозначать
σ 1, σ 2, σ 3,
при этом полагают, что в алгебраическом смысле: σ 1 > σ 2 > σ 3
Виды напряженных состояний
Вид напряженного состояния определяется
количеством действующих главных напряжений.
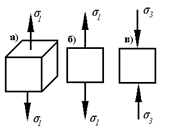
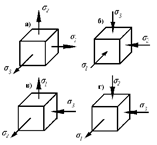
1). Линейное (одноосное) напряженное состояние
К граням элементарного параллелепипеда приложено только одно нормальное напряжение.
Остальные два равны нулю.
Если нормальное напряжение растягивающее – имеем наибольшее главное напряжение σ 1 (рис. а).
Схемы на рис. а и рис. б аналогичны – во втором случае вместо параллелепипеда изображена одна плоская грань.
На рис. в – приложено только одно сжимающее нормальное напряжение, поэтому обозначаем его σ 3.
2) Плоское (двухосное) напряженное состояние
По любым двум взаимно перпендикулярным граням параллелепипеда (в нашем случае по граням произвольного плоского элемента) могут быть приложены два одинаковых по величине и направлению нормальных напряжения.
Если оба растягивающих (рис. а), то обозначаем их σ 1 и σ 2, (σ 3=0),
если оба сжимающих (рис. б), то σ 2 и σ 3, (σ 2=0).
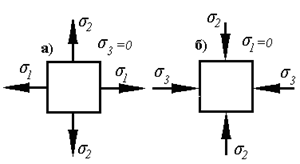
Но может быть и вариант (рис. в).
В этом случае одно нормальное напряжение растягивающее, другое – сжимающее.
Наибольшее по величине (в алгебраическом смысле) нормальное напряжением обозначается σ 1 наименьшее σ 3 σ 2=0.
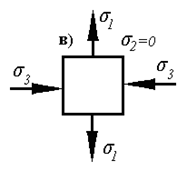
3) Объемное (трехосное) напряженное состояние
В этом случае вариантов приложения напряжений еще больше.
Подходы к обозначениям главных напряжений рассмотрены достаточно подробно выше.
 В большинстве случаев в инженерных расчетах встречаются линейное или плоское напряженные состояния.
В большинстве случаев в инженерных расчетах встречаются линейное или плоское напряженные состояния.
 Запишем выражения для шарового тензора и девиатора через главные напряжения, обозначив
Запишем выражения для шарового тензора и девиатора через главные напряжения, обозначив
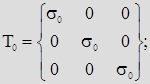 | 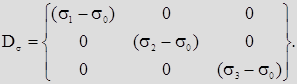 |
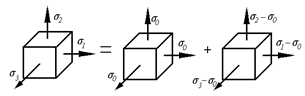
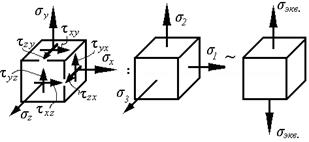
Руководствуясь принципом суперпозиции, покажем схемы напряженных состояний, определяющих, соответственно, изменение объема и изменение формы элементарного параллелепипеда.
Инварианты напряженного состояния. Интенсивность напряжений. Наибольшие касательные напряжения.
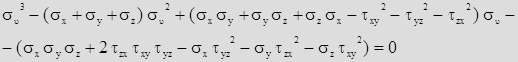 Главные напряжения являются корнями кубического уравнения (подробности получения его опускаем):
Главные напряжения являются корнями кубического уравнения (подробности получения его опускаем):
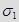 |
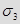 Максимальное главное напряжение (в алгебраическом смысле) –
Максимальное главное напряжение (в алгебраическом смысле) –
Минимальное главное напряжение –
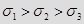 |
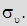 Значения корней кубического уравнения зависят от коэффициентов, стоящих при различных степенях
Значения корней кубического уравнения зависят от коэффициентов, стоящих при различных степенях
В свою очередь, значения этих коэффициентов не зависят от выбора системы координат:
они инвариантны к системе координат.
Их называют: инварианты напряженного состояния S
(соответственно, первый, второй, третий инварианты):
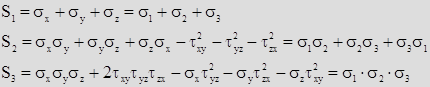 |
Тогда кубическое уравнение примет вид:
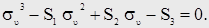 |
Интенсивность напряжений
В сопромате и теории упругости при проведении расчетов используются так называемые теории прочности (будут рассмотрены ниже).
При разработке этих теорий вводится гипотеза о преимущественном влиянии на прочность материала того или иного фактора (критерия). Таким образом, предусматривается возможность проверки этого критерия сопоставлением данного (сложного) напряженного состояния с простым (обычно с одноосным).
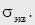 При этом устанавливается значение эквивалентного (расчетного) напряжения
При этом устанавливается значение эквивалентного (расчетного) напряжения
В теории упругости эквивалентные напряжения называют интенсивностью напряжений
 |
Наибольшие касательные напряжения
Анализ напряженных состояний позволяет определить величину максимальных касательных напряжений.
Эти напряжения (доказано в теории упругости и подтверждается экспериментально) «ответственны» за пластическую деформацию тела.
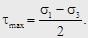 Максимальное значение касательных напряжений определяется полуразностью экстремальных значений главных напряжений:
Максимальное значение касательных напряжений определяется полуразностью экстремальных значений главных напряжений: