
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа №1
|
|
(только для студентов заочной формы, со сроком обучения 5 лет)
Вариант 1
1. Вычислить матрицу  , где
, где  и
и 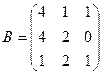 .
.
2. Даны матрицы:
 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
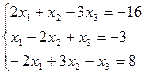
4. Даны векторы 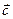 (0; 1; -1) и
(0; 1; -1) и 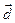 (1; 1; -4). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(1; 1; -4). Найти длины диагоналей и площадь параллелограмма, построенного на векторах 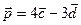 и
и 
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
6. Даны уравнения сторон треугольника 2х-5у=3, х+3у=7 и 3х-2у+1=0.Написать уравнение медианы и высоты, проведенных на сторону 2х-5у=3. Сделать чертеж.
7. Построить графики функций:  .
.
8. Вычислить пределы функций:
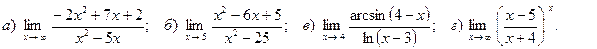
9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.

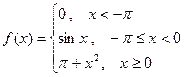
10. Найти производные функций:.
а)  , б)
, б) 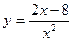 , в)
, в)  .
.
11. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
12. Провести полное исследование функции  и построить её график.
и построить её график.
Вариант 2
1. Вычислить матрицу  , где
, где 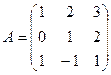 и
и 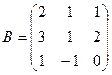 .
.
2. Даны матрицы:
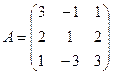 и
и 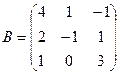 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение. 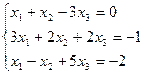
4. Даны векторы  (1; 2; 0) и
(1; 2; 0) и  (0; 3; -1). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(0; 3; -1). Найти длины диагоналей и площадь параллелограмма, построенного на векторах  и
и 
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5)уравнение плоскостей  и
и  .
.
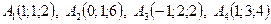 .
.
6. Даны уравнения сторон треугольника 2х-5у=3, х+3у=7 и 3х-2у+1=0.Написать уравнение медианы и высоты, проведенных на сторону х+3у=7. Сделать чертеж.
7. Построить графики функций: 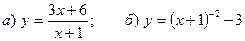 .
.
8. Вычислить пределы функций:

9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.

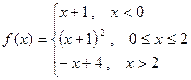
10. Найти производные функций:
 а)
а) 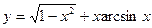 , б)
, б) 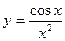 , в)
, в) 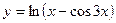 .
.
11. Вычислить предел 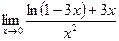 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12. Провести полное исследование функции  и построить её график.
и построить её график.
Вариант 3
1. Вычислить матрицу 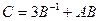 , где
, где  и
и 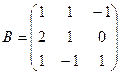 .
.
2. Даны матрицы:
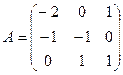 и
и 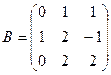 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение 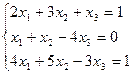
4. Даны векторы 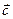 (1; 0; -1) и
(1; 0; -1) и  (-4; 1; 2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(-4; 1; 2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах  и
и 
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
6. Даны уравнения сторон треугольника 2х-5у=3, х+3у=7 и 3х-2у+1=0. Написать уравнение медианы и высоты, проведенных на сторону 3х-2у+1=0. Сделать чертеж.
7. Построить графики функций: 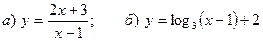 .
.
8. Вычислить пределы функций:
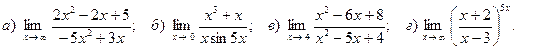
9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.

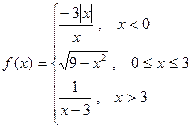
10. Найти производные функций:
 а)
а) 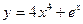 , б)
, б)  , в)
, в) 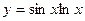 .
.
11.Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
12.Провести полное исследование функции и построить её график: 
 .
.
Вариант 4
1. Вычислить матрицу 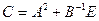 , где
, где  и
и  .
.
2. Даны матрицы:
 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение 
4. Даны векторы  (2; 3; -2) и b
(2; 3; -2) и b 
 (0; 1; 3). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(0; 1; 3). Найти длины диагоналей и площадь параллелограмма, построенного на векторах 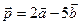 и
и 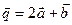
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
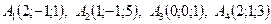 .
.
6. Даны уравнения сторон треугольника х-3у+5=0, 3х+4у+2=0 и 5х-2у-14=0. Написать
уравнение медианы и высоты, проведенных на сторону х-3у+5=0. Сделать чертеж.
7. Построить графики функций:  .
.
8. Вычислить пределы функций:
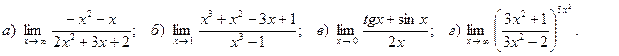
9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


10. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в)  .
.
11. Вычислить предел 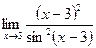 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12. Провести полное исследование функции и построить её график:

 .
.
Вариант 5
1. Вычислить матрицу 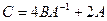 , где
, где 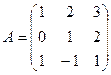 и
и 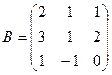 .
.
2. Даны матрицы:
 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение 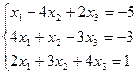
4. Даны векторы 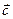 (1; 5; 0) и
(1; 5; 0) и 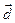 (1; -2; 3). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(1; -2; 3). Найти длины диагоналей и площадь параллелограмма, построенного на векторах 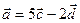 и
и 
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
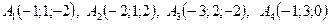 .
.
6. Даны уравнения сторон треугольника х-3у+5=0, 3х+4у+2=0 и 5х-2у-14=0. Написать уравнение медианы и высоты, проведенных на сторону 3х+4у+2=0. Сделать чертеж.
7. Построить графики функций: 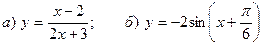 .
.
8. Вычислить пределы функций:

9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


10.Найти производные функций:
 а)
а) 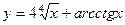 , б)
, б)  , в)
, в) 
11. Вычислить предел 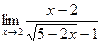 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12. Провести полное исследование функции и построить её график:

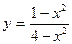 .
.
Вариант 6
1. Вычислить матрицу  , где
, где  и
и 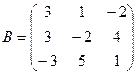 .
.
2. Даны матрицы:
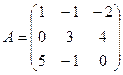 и
и 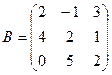 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение 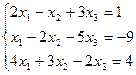
4. Даны векторы  (1; 0; 5) и
(1; 0; 5) и  (3; -1; 2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(3; -1; 2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах  и
и 
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
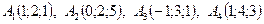 .
.
6. Даны уравнения сторон треугольника х-3у+5=0, 3х+4у+2=0 и 5х-2у-14=0. Написать уравнение медианы и высоты, проведенных на сторону 5х-2у-14=0. Сделать чертеж.
7. Построить графики функций: 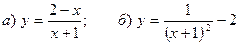 .
.
8. Вычислить пределы функций:

9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


10. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
11. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
12.Провести полное исследование функции и построить её график:

 .
.
Вариант 7
1. Вычислить матрицу 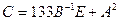 , где
, где  и
и 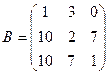 .
.
2. Даны матрицы:
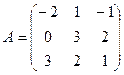 и
и 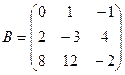 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
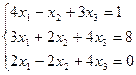
4. Даны векторы 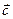 (3; 1-1) и
(3; 1-1) и 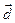 (0; 1; 1). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(0; 1; 1). Найти длины диагоналей и площадь параллелограмма, построенного на векторах  и
и 
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
6. Даны уравнения сторон треугольника 5х+12у+11=0, 4х-3у-29=0 и х+15у-23=0. Написать уравнение медианы и высоты, проведенных на сторону 5х+12у+11=0. Сделать чертеж.
7. Построить графики функций:  .
.
8. Вычислить пределы функций:

9.Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.

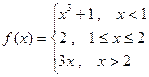
10. Найти производные функций:
а)  , б)
, б)  , в)
, в) 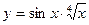
11.Вычислить предел 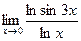 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12.Провести полное исследование функции 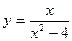 и построить её график.
и построить её график.
Вариант 8
1. Вычислить матрицу  , где
, где  и
и 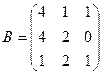 .
.
2. Даны матрицы:
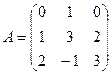 и
и 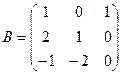 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
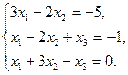
4. Даны векторы 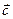 (1; -1; 3) и
(1; -1; 3) и 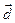 (2; 1; 0). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(2; 1; 0). Найти длины диагоналей и площадь параллелограмма, построенного на векторах  и
и 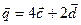
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
6. Даны уравнения сторон треугольника 5х+12у+11=0, 4х-3у-29=0 и х+15у-23=0.Написать уравнение медианы и высоты, проведенных на сторону 4х-3у-29=0. Сделать чертеж.
7. Построить графики функций: 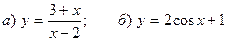 .
.
8. Вычислить пределы функций:
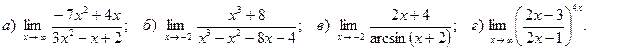
9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


10. Найти производные функций:
 а)
а)  , б)
, б) 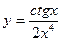 , в)
, в) 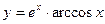
11. Вычислить предел 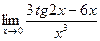 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12. Провести полное исследование функции и построить её график:

 .
.
Вариант 9
1. Вычислить матрицу  , где
, где  и
и 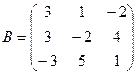 .
.
2. Даны матрицы:
 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение 
4. Даны векторы 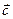 (2; 1; 4) и
(2; 1; 4) и 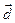 (0; 3; -3). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(0; 3; -3). Найти длины диагоналей и площадь параллелограмма, построенного на векторах  и
и 
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
6. Даны уравнения сторон треугольника 5х+12у+11=0, 4х-3у-29=0 и х+15у-23=0. Написать уравнение медианы и высоты, проведенных на сторону 5х+12у+11=0. Сделать чертеж.
7. Построить графики функций: 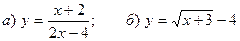 .
.
8. Вычислить пределы функций:

9.Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


10.Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 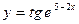
11. Вычислить предел 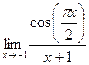 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12. Провести полное исследование функции и построить её график:

 .
.
Вариант 10
1. Вычислить матрицу 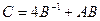 , где
, где  и
и 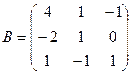 .
.
2. Даны матрицы:
 и
и 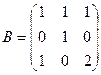 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение 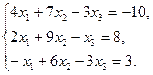
4. Даны векторы 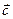 (3; 4; 1) и
(3; 4; 1) и 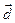 (0; 2; -2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(0; 2; -2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах 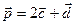 и
и 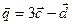
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
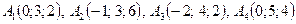 .
.
6. Даны уравнения сторон треугольника х+у+1=0, 3х-2у-17=0 и 2х+7у-3=0. Написать уравнение медианы и высоты, проведенных на сторону х+у+1=0. Сделать чертеж.
7. Построить графики функций:  .
.
8. Вычислить пределы функций:

9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


10. Найти производные функций:
 а)
а) 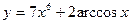 , б)
, б)  , в)
, в) 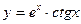
11. Вычислить предел 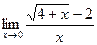 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12.Провести полное исследование функции и построить её график:
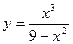 .
.
Демонстрационный вариант контрольной работы № 1
1. Вычислить матрицу 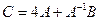 , где
, где 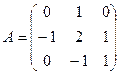 и
и 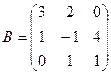 .
.
2. Даны матрицы:
 и
и 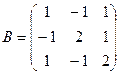 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. Даны векторы 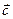 (1; 2; 3) и
(1; 2; 3) и 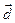 (-1; 3; 2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах
(-1; 3; 2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах  и
и 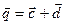
5. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
6. Даны уравнения сторон треугольника х-3у+12=0, 13х+2у-49=0 и 11х+8у+9=0. Написать уравнение медианы и высоты, проведенных на сторону 13х+2у-49=0 Сделать чертеж.
7. Построить графики функций: 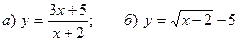 .
.
8. Вычислить пределы функций:

9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.

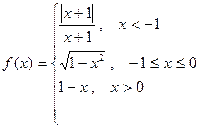
10.Найти производные функций:
 а)
а) 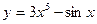 , б)
, б) 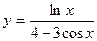 , в)
, в) 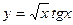
11. Вычислить предел 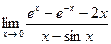 с помощью правила Лопиталя.
с помощью правила Лопиталя.
12. Провести полное исследование функции  и построить её график.
и построить её график.
Решение демонстрационного варианта контрольной работы №1