Решение задачи 5

а) 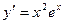- это уравнение с разделяющимися переменными.

Разделим переменные, т.е. получим уравнение .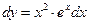

Интегрируем обе части полученного уравнения

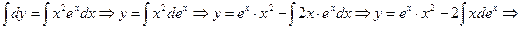
- общее решение.

б) 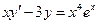- это линейное дифференциальное уравнение 1 – ого порядка.

Первый способ: метод подстановки. Пусть 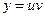, тогда . Подставив в исходное уравнение, получим 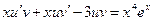. Группируем таким образом, чтобы в скобках была только одна функция 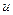или , т.е. 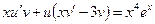(можно 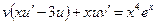). Далее выбираем функцию так, чтобы выражение в скобках обращалось в нуль, т.е.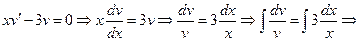

.

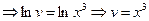Подставим найденное 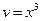в уравнение 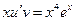, получим .

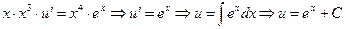Общее решение уравнение .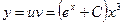

Второй способ. Метод вариации произвольной постоянной. Предварительно решаем линейное уравнение .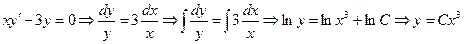

Затем решение исходного уравнения ищем в виде 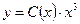, т.е. заменяем константу неизвестной функцией. Подставляем это решение в уравнение, получим

.

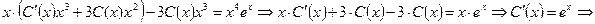
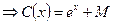Искомое общее решение уравнение .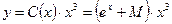

Ответ: 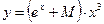.