Решение задачи 12

Исследовать и построить график функции

Решение.

1. Область определения функции D(у)= .

1. Находим точки пересечения графика функции с осями координат: если х=0, то у=0; если у=0, то х=0. Таким образом, график проходит через начало координат
2. Функция не является периодической, так как не существует такого положительного числа Т, что у(х+Т)=у(х).
3. Функция является нечётной, т.к.

1) область определения симметрична относительно начала координат, 2) у(-х)= -у(х).

1. Определим асимптоты графика:

а) Вертикальные асимптоты.

Точки х= 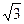и х= - 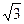являются точками разрыва функции. Так как 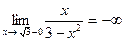и 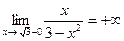, то прямая х= 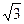служит вертикальной асимптотой графика функции. Аналогично найдём односторонние пределы в точке х= - :

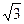и 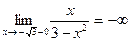, следовательно, прямая х= - 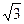также является вертикальной асимптотой графика функции.

б) горизонтальные асимптоты.

Для нахождения горизонтальной асимптоты вычислим предел функции на бесконечности:

, итак, прямая у=0 – горизонтальная асимптота.

в) Наклонные асимптоты:

у=кх+b – уравнение наклонной асимптоты

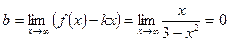
наклонной асимптоты нет (она совпадает с горизонтальной у=0).

1. Исследуем функцию на монотонность и экстремум:

;

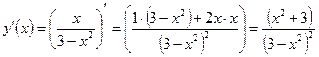Найдём критические точки из услови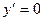й или 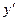не существует:

равенство не выполняется ни при каких х;

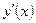не существует при х= 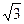и х= - .

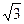Итак, критические точки: х= 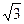и х= - .

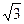Составим таблицу

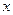
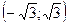
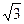
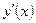
	+	Не существует	+	Не существует	+
		Не существует		Не существует
	возрастает		возрастает		возрастает

1. Исследуем функцию на выпуклость и вогнутость, найдём точки перегиба:

.

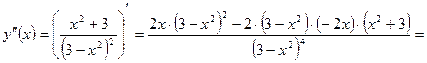
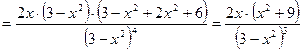Определим критические точки для второй производной:

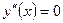, т.е. , откуда ;

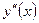не существует при .

Составим таблицу:

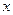
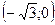
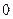
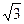
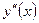
	+	Не существует	_		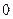+	Не существует	_
		Не существует		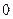		Не существует
	вогнутая		выпуклая	Точка перегиба	вогнутая		выпуклая

8. Найдём значения функции в некоторых точках: , , , .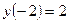

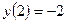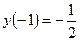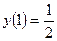9. Построим график функции
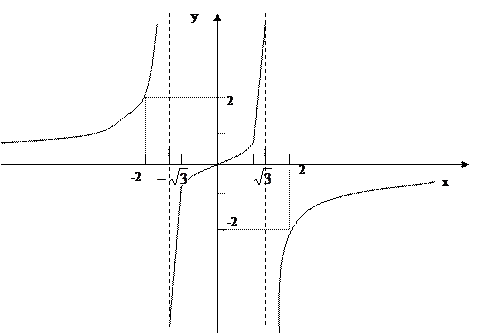