Решение задачи 10

а)

Это положительный числовой ряд, можно применить один из пяти достаточных признаков сходимости.

Проверяем сходимость ряда по признаку Даламбера. Т.к. общий член ряда 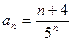, то, заменяя в выражении n – го члена n на n+1, находим

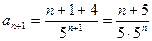. Затем ищем предел отношения последующего члена 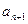к предыдущему при

.

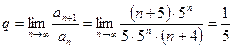Итак, , следовательно, ряд сходится.

б)

Это знакочередующийся ряд. Воспользуемся признаком Лейбница. Для этого нам надо показать, что

1) члены ряда по модулю убывают, т.е.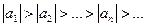

2)

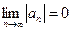
Проверим эти условия:

1)

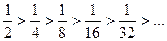, т.е. первое условие выполняется.

2) 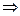выполняется второе условие.

Итак, условия 1, 2 выполняются, следовательно, ряд сходится.

Выясним, сходится он абсолютно или условно, для этого исследуем ряд, составленный из модулей : - бесконечно убывающая геометрическая прогрессия 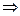ряд сходится 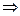исходный ряд сходится абсолютно.

Ответ: а) ряд сходится; б) ряд сходится абсолютно.