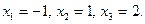Решение задачи 3

1. Метод Крамера

Вычислим определитель системы: .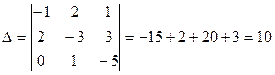

Найдём :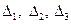

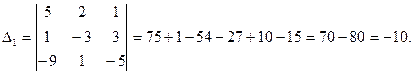
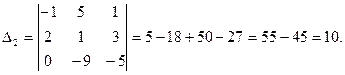
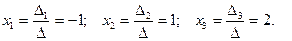
Проверка корней:

подставим полученные значения неизвестных в систему

Ответ: .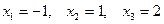

2. Метод обратной матрицы (матричный метод)

Запишем систему линейных уравнений в матричной форме: 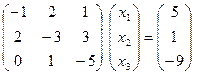; То есть АХ=В, умножая слева обе части уравнения на А^-1, получаем , где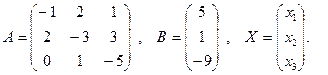

Так как определитель матрицы системы отличен от нуля: 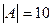, то матрица 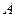имеет обратную. Для нахождения обратной матрицы 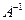вычислим алгебраические дополнения элементов матрицы .

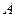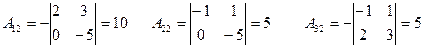
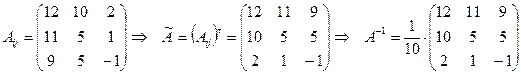
Правильность нахождения обратной матрицы проверим средствами матричного исчисления:

АА^-1=А^-1А=Е.

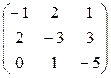
= (Убедитесь в истинности этого равенства самостоятельно).

Матричное решение системы имеет вид

откуда следует (из условия равенства двух матриц), что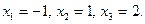

Ответ: .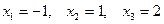

3. Метод Гаусса

Составим расширенную матрицу и применим к ней преобразования:

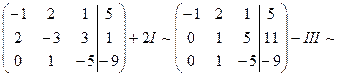
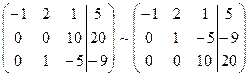
Итак, расширенная матрица с помощью элементарных преобразований сведена к ступенчатому виду. Перейдём к равносильной системе

отсюда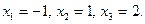

Ответ: