
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа № 1с
|
|
(только для студентов заочной формы, со сроком обучения 3 года)
Вариант 1
1. Вычислить матрицу  , где
, где  и
и 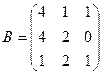 .
.
2. Найти решение системы линейных уравнений методом Крамера, методом обратной матрицы, методом Гаусса.
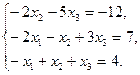
3. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
4. Вычислить пределы функций:
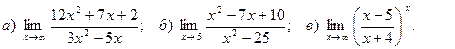

5. Найти производные функций:
а)  , б)
, б) 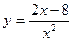 , в)
, в)  .
.
6.Провести полное исследование функции  и построить её график.
и построить её график.
7. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а)  , б)
, б) 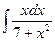 , в)
, в)  . г)
. г) 
8. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

 .
.
9. Найти частные производные первого и второго порядка функций:
а) 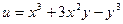 б)
б) 
10. Исследовать на экстремум функцию  .
.
11. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
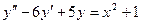 ;
;  .
.
12. Найти радиус и интервал сходимости степенного ряда.
Исследовать сходимость ряда на концах интервала сходимости.

Вариант 2
1. Вычислить матрицу 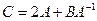 , где
, где 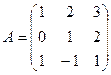 и
и 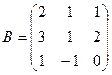 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
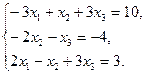
3. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
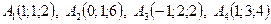 .
.
4. Вычислить пределы функций:
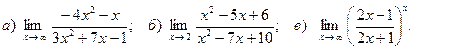
5. Найти производные функций:
 а)
а) 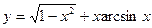 , б)
, б) 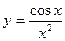 , в)
, в) 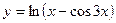 .
.
6. Провести полное исследование функции  и построить её график.
и построить её график.
7.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а)  , б)
, б) 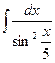 , в)
, в)  . г)
. г) 
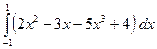
8. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

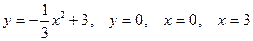 .
.
9.Найти частные производные первого и второго порядка функций:
а)  б)
б) 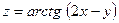
10. Исследовать на экстремум функцию  .
.
11. Найти общее решение дифференциального уравнения и частное решение,
удовлетворяющее заданным начальным условиям:
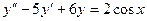 ;
;  .
.
12. Найти радиус и интервал сходимости степенного ряда.
Исследовать сходимость ряда на концах интервала сходимости.

Вариант 3
1. Вычислить матрицу 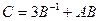 , где
, где  и
и 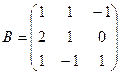 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.

3. По координатам вершин пирамиды  : А1(-1; -2; 1) А2(-2; -2; 5) А3(-3; -1; 1) А4(-1; 0; 3) найти:
: А1(-1; -2; 1) А2(-2; -2; 5) А3(-3; -1; 1) А4(-1; 0; 3) найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
4. Вычислить пределы функций:
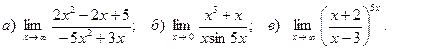
5. Найти производные функций:
 а)
а) 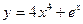 , б)
, б)  , в)
, в) 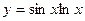
6.Провести полное исследование функции и построить её график: 
 .
.
7.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а)  , б)
, б) 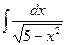 , в)
, в)  , г)
, г) 
8.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

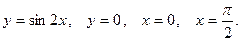
9. Найти частные производные первого и второго порядка функций:
а) 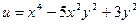 б)
б) 
10. Исследовать на экстремум функцию 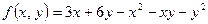 .
.
11. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: 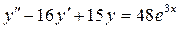 ;
;  .
.
12. Найти радиус, интервал и область сходимости ряда: 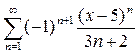 .
.
Вариант 4
1. Вычислить матрицу 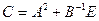 , где
, где  и
и  .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
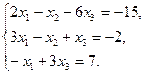
3. По координатам вершин пирамиды  : А1(2; -1; 1) А2(1; -1; 5) А3(0; 0; 1) А4(2; 1; 3) найти:
: А1(2; -1; 1) А2(1; -1; 5) А3(0; 0; 1) А4(2; 1; 3) найти:
1)длины рёбер  и
и  ;
;
6) угол между рёбрами  и
и  ;
;
7) площадь грани  ;
;
8) объём пирамиды;
9) уравнение плоскостей  и
и  .
.
4. Вычислить пределы функций:
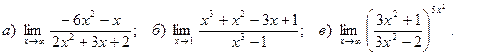
5.Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
6.Провести полное исследование функции и построить её график:

 .
.
7. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а)  , б)
, б) 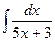 , в)
, в) 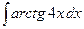 .
.
8. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.


9. Найти частные производные первого и второго порядка функций:
а)  б)
б) 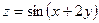
10. Исследовать на экстремум функцию 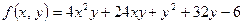 .
.
11. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: 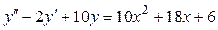 ;
; 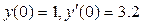 .
.
12. Найти радиус, интервал и область сходимости ряда: 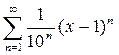 .
.
Вариант 5
1. Вычислить матрицу 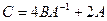 , где
, где 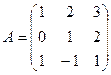 и
и 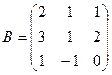 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
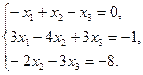
3. По координатам вершин пирамиды  А1(-1; 1; -2) А2(-2; 1; 2) А3(-3; 2; -2) А4(-1; 3; 0) найти:
А1(-1; 1; -2) А2(-2; 1; 2) А3(-3; 2; -2) А4(-1; 3; 0) найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
4. Вычислить пределы функций:

5.Найти производные функций:
 а)
а) 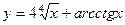 , б)
, б)  , в)
, в) 
6. Провести полное исследование функции и построить её график:

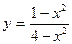 .
.
7.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
.
а)  , б)
, б) 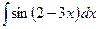 , в)
, в) 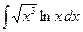 , г)
, г) 
8.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

 .
.
9. Найти частные производные первого и второго порядка функций:
а) 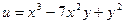 б)
б) 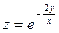
10. Исследовать на экстремум функцию 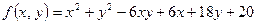 .
.
11. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: 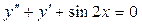 ;
;  .
.
12. Найти радиус, интервал и область сходимости ряда:  .
.
Вариант 6
1. Вычислить матрицу  , где
, где  и
и 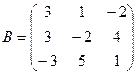 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.

3. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
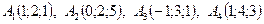 .
.
4. Вычислить пределы функций:
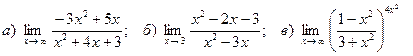
5.Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
6.Провести полное исследование функции и построить её график:

 .
.
7. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а) 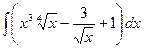 , б)
, б)  , в)
, в) 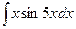 , г)
, г) 
8.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

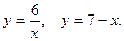
9.Найти частные производные первого и второго порядка функций:
а)  б)
б) 
10. Исследовать на экстремум функцию 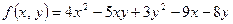 .
.
11. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: 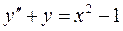 ;
; 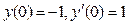 .
.
12. Найти радиус, интервал и область сходимости ряда: 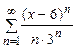 .
.
Вариант 7
1. Вычислить матрицу 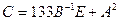 , где
, где  и
и 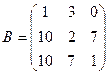 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
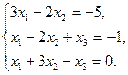
3. По координатам вершин пирамиды  найти:
найти:
6) длины рёбер  и
и  ;
;
7) угол между рёбрами  и
и  ;
;
8) площадь грани  ;
;
9) объём пирамиды;
10) уравнение плоскостей  и
и  .
.
 .
.
4. Вычислить пределы функций:
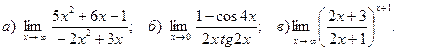
5.Найти производные функций:
а)  , б)
, б)  , в)
, в) 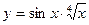
6.Провести полное исследование функции 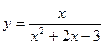 и построить её график.
и построить её график.
7.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а) 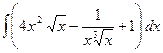 , б)
, б) 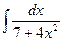 , в)
, в) 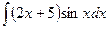 , г)
, г) 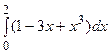
8.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
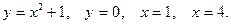
9. Найти частные производные первого и второго порядка функций:
а)  б)
б) 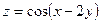
10.Исследовать на экстремум функцию 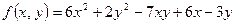 .
.
11. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям:  ;
; 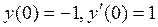 .
.
12. Найти радиус, интервал и область сходимости ряда: 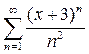 .
.
Вариант 8
1. Вычислить матрицу  , где
, где  и
и 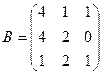 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.

3. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
4. Вычислить пределы функций:
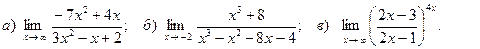
5.Найти производные функций:
 а)
а)  , б)
, б) 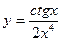 , в)
, в) 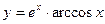
6.Провести полное исследование функции и построить её график:

 .
.
7.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а) 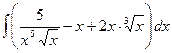 , б)
, б) 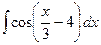 , в)
, в) 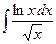 , г)
, г) 
8.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

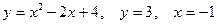 .
.
9.Найти частные производные первого и второго порядка функций:
а) 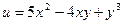 б)
б) 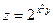
10. Исследовать на экстремум функцию  .
.
11. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям:  ;
; 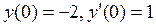 .
.
12. Найти радиус, интервал и область сходимости ряда: 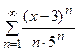 .
.
Вариант 9
1. Вычислить матрицу 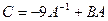 , где
, где  и
и 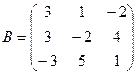 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
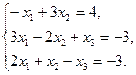
3. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
4. Вычислить пределы функций:
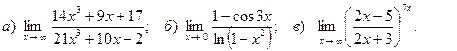
5.Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 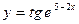
6.Провести полное исследование функции и построить её график:

 .
.
7.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а)  , б)
, б) 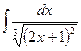 , в)
, в) 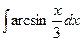 , г)
, г) 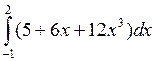
8.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
 .
.
9.Найти частные производные первого и второго порядка функций:
а) 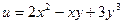 б)
б) 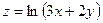
10. Исследовать на экстремум функцию 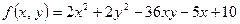 .
.
11. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
 ;
;  ,
, 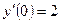 .
.
12. Найти радиус, интервал и область сходимости ряда: 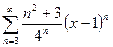
Вариант 10
1. Вычислить матрицу  , где
, где  и
и 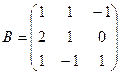 .
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
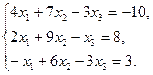
3. По координатам вершин пирамиды  найти:
найти:
1)длины рёбер  и
и  ;
;
2)угол между рёбрами  и
и  ;
;
3)площадь грани  ;
;
4)объём пирамиды;
5)уравнение плоскостей  и
и  .
.
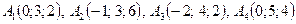 .
.
4. Вычислить пределы функций:
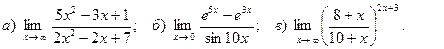
5.Найти производные функций:
 а)
а) 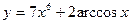 , б)
, б)  , в)
, в) 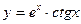
6.Провести полное исследование функции 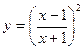 и построить её график.
и построить её график.
7.Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а, б, в) проверить дифференцированием. Найти определённый интеграл (г).
 а)
а)  , б)
, б) 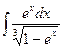 , в)
, в) 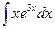 , г)
, г) 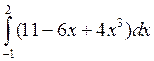
8.Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

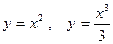 .
.
9. Найти частные производные первого и второго порядка функций:
а)  б)
б) 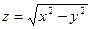
10. Исследовать на экстремум функцию  .
.
11. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
 ;
;  ,
, 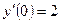 .
.
12. Найти радиус, интервал и область сходимости ряда:  .
.
Для решения контрольной работы № 1с можно воспользоваться соответствующими заданиями демонстрационных вариантов, рассмотренных в контрольных работах № 1, 2.
6. Выполнение и оформление контрольной работы
Контрольная работа состоит из 10 вариантов, по 12 заданий в каждом, варианты выбираются студентом по последней цифре номера зачетной книжки.
При выполнении работы студенты знакомятся с рекомендуемой основной и дополнительной литературой, с электронными ресурсами образовательного сайта ВСЭИ.
Структура контрольных работ: с новой страницы – номер и содержание задания, ниже полное решение задачи, необходимые пояснения, чертежи, список литературы (введение, приложения не требуются).
Оформление контрольных работ должно соответствовать требованиям, приведенным в методическом пособии «Выполнение контрольных и курсовых работ: Методические рекомендации для студентов, обучающихся по ФГОС-3» (ВСЭИ, 2013).
7. Учебно-методическое обеспечение
А. Основная литература
1. Высшая математика для экономических специальностей: учебник и практикум. Ч. 1, 2 / под ред. Н.Ш. Кремер. – М.: Высшее образование, 2006.
2. Линьков, В.М.Высшая математика в примерах и задачах. Компьютерный практикум: учеб. пособие / В.М. Линьков. – М.: Финансы и статистика, 2006.
3. Самаров, К.Л.Задачи с решениями по высшей математике и математическим методам в экономике: учеб. пособие. – М.: Дашков и Кº, 2007.
Б. Дополнительная литература
1. Александров П.С. Лекции по аналитической геометрии, пополненные необходимымисведениями из алгебры. – М.: Наука, 1968.
2. Баврин И.И. Высшая математика. - М.: Академия, 2002.
3. Бортаковский А.С., Пантелеев А.В. Линейная алгебра в примерах и задачах. – М.: Высшая школа, 2005.
4. Бурмистрова Е.Б., Лобанов С.Г. Линейная алгебра с элементами аналитической геометрии. – М.: Изд-во ВШЭ, 2007.
5. Бутузов и др. Математический анализ в вопросах и задачах: Учеб. пособие. – М.: Высшая школа, 1984.
6. Виленкин И.Я., Куницына Е.С., Мордкович А.Г. Математический анализ. Интегральное исчисление. - М.: Просвещение, 1979.
7. Гельфанд И.М. Лекции по линейной алгебре. – М.: Добросвет, 2006.
8. Зайцев И.А. Высшая математика. - М.: Высшая школа, 1998.
9. Ильин В.А., Поздняк Э.Г. Основы математического анализа. Ч. 2. - М.: Наука, 1973.
10. Левин М.Н., Рапопорт А.Н., Рапопорт Л.Д. Сборник задач по математике для экономистов. - Киров, 1998.
11. Лунгу К.Н. Сборник задач по высшей математике. - М.: Айрис – Пресс, 2006.
12. Поршнев С.В. Вычислительная математика. – СПб.: «БХВ - Петербург», 2004.
13. Рапопорт А.Н. Высшая математика. Образовательный курс. - Киров, 2000.
14. Сборник задач по высшей математике для экономистов: учебное пособие / Под ред. В.И. Ермакова. - М.: ИНФРА-М, 2008.
15. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. - М.: Наука, 2004
16. Шипачев В.С. Задачник по высшей математике. - М.: Высшая школа, 2004.
В. Программное обеспечение
Не предусмотрено.
Г. Базы данных, информационно-справочные и поисковые системы
Автоматизированная информационно-библиотечная система «Марк».
ЭБС IPRbooks: www.iprbookshop.ru.
ЭБС ВСЭИ: https://edu/vs_library/index.php
Глушкова Августа Игоревна