Решение задачи 6

Чтобы составить уравнения высоты и медианы, найдем координаты вершин треугольника АВС. Для этого решим 3 системы:

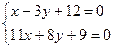
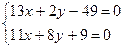
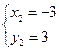
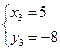
А(3; 5) В(-3; 3) С(5-8)

Найдем уравнение медианы ВД. По формуле координаты середины Д отрезка АС:

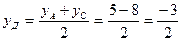
Воспользуемся уравнением прямой, проходящей через две данные точки

В (х₁, у₁) и Д (х₂, у₂)

Подставляя координаты точек Д(4; ) и В(-3; 3) в уравнение, получим:

или 9х+14у-15=0 – уравнение медианы ВД

Найдем уравнение высоты ВН. Для этого воспользуемся уравнением прямой, проходящей через данную точку В (х₀; у₀) в данном направлении у-у₀=k(х-х₀). Так как В (-3; 3), получаем

у-3=k(х+3). Чтобы найти k, воспользуемся условием перпендикулярности двух прямых

у А(3; 5)

В(-3; 3) Н

х

Д

С(5; -8)

Уравнение АС: 13х+2у-49=0 или , значит , тогда 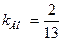. Подставляя в уравнение пучка прямых, получаем у-3= или 13у-2х-45=0 - уравнение высоты ВН.