Лекция. Сызықтық кеңістіктер және олардың мысалдары.Сызықтық кеңістіктің өлшемі мен базисі.

Табиғ аты ә ртү рлі болып келе беретін х, у, z,... элементтерінің R жиынын сызық ты кең істік деп атаймыз, егер R жиыны ү шін келесі ү ш шарт орындалар болса:

1. R жиынының кез келген х, у элементтеріне олардың қ осындысы деп аталып, былай белгіленетін z=x + y элементі сә йкес қ ойылғ ан, z R.

2. R жиынының кез келген х элементіне жә не кез келген l нақ ты санына х элементінің l санына кө бейтіндісі деп аталып, былай бел-гіленетін u =lx элементі сә йкес қ ойылғ ан, u R.

3. Анық талғ ан екі амал келесі сегіз аксиоманы қ анағ аттанды-рады:

1°. х+у = y+x;

2°. (x+y)+z = x+(y+z);

3°. x+q = x болатындай нө лдік элемент бар;

4°. кез келген х элементіне қ арама-қ арсы х¢ элементі бар жә не

х+х¢ = q;

5°. 1х = x;

6°. l (m х) = (lm) х;

7°. (l+m) х = l х+m х;

8°. l(х+у) = l х+l у;

Cызық тық кең істікте нө лдік элемент жалғ ыз жә не ол 0х = q тү рінде болады.

Сондай-ақ кез келген сызық ты кең істікте ә рбір х элементінің жалғ ыз қ арама-қ арсы элементі бар жә не ол (-1) x тү рінде болады.

Сызық ты кең істік элементтерін ә детте вектор деп атайды.

Есеп шығ ару барысында берілген жиында анық талғ ан екі амалғ а назар аударып, ол амалдар ү шін жоғ арыдағ ы сегіз аксиоманың орындалуын тексеру керек. Берілген жиында екі амалдың бірі анық талмағ ан, яки осы сегіз аксиоманың біреуі орындалмаса, ондай жиын сызық ты кең істік болмайды.

Нақ ты сан ө сіндегі кесінді немесе интервал, нақ ты сандарғ а қ олданылатын кә дімгі арифметикалық амалдарды пайдаланар болсақ, сызық ты кең істік болмайды. Сан ө сінен [0, 1] кесіндісін алайық. Бұ л жиында қ осу амалы анық талмағ ан. Ө йткені, осы кесіндінің екі элементі болып табылатын 0, 5 жә не 1 сандарының қ осындысы 1, 5 саны бұ л жиында жатпайды, яғ ни, қ осу амалы анық талмағ ан.

Енді мысалдар қ арастырайық.

1-мысал. R жиыны тү ріндегі реттелген сың арлы нақ ты сандардан тұ рады.

Мұ ндағ ы 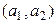мен 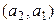ә ртү рлі элементтер. Бұ л жиында амалдар былай анық талғ ан

.

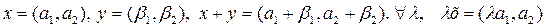Осы R жиыны сызық ты кең істік бола ма?

Шешуі. Қ осу амалы алғ ашқ ы екі аксиоманы қ анағ аттандырады.

1. х + у = у + х, ө йткені,

ал 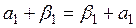, 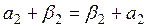себебі дегендеріміз нақ ты сандар. Осы себепті 2° аксиома да орындалады. 3° аксиомағ а келейік. Нө лдік элемент 0х = q тү рінде болады дедік. Ендеше 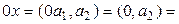q нө лдік элемент болуы керек. Бірақ, х+q = .

Яғ ни 3° аксиома орындалмайды, сондық тан бұ л жиын сызық ты кең істік болмайды. Осы жерде 7°-аксиоманың да орындалмайтын-дығ ын атап ө тейік

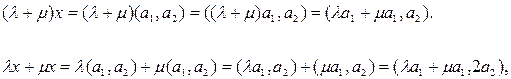
яғ ни .

2 - мысал. Алдың ғ ы есепте қ осу амалы сақ талып, элементті санғ а кө бейту амалын былай анық тайық

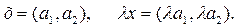
Сонда R жиыны сызық ты кең істік бола ма?

Шешуі. Бұ л жағ дайда R жиыны сызық ты кең істік болады. Алғ ашқ ы екі аксиоманың орындалуын жоғ арыда тексердік.

3° аксиома орындалады:

q.

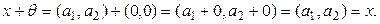
Сондай-ақ 7° аксиома да орындалады.

.

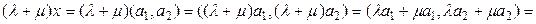
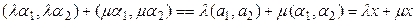5°, 6°, 8° аксиомалардың орындалуы да осығ ан ұ қ сас тексеріледі. Жоғ арыда қ арама-қ арсы элемент тү рінде болады дедік. Ендеше 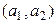= () қ арама-қ арсы элемент болады, ө йткені

.

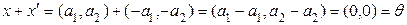Сонымен, 4° аксиома да орындалады екен.

3 – мысал. Тағ ы бір мысал қ арастырайық. жиынында екі элемент-ті қ осу амалы мен элементті нақ ты санғ а кө бейту амалы ә деттегі нақ ты сандарғ а қ олданылып жү рген амал ретінде анық талсын. Онда бұ л жиын сызық ты кең істік болмайды, ө йткені жиынынан алынғ ан кез келген элементті теріс таң балы санғ а кө бейткенде теріс таң балы сан аламыз. Ал мұ ндай сан жиынында жатпайды, яғ ни жиынында элементті кез келген l нақ ты санына кө бейту амалы анық талмағ ан.