Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гильберт кеңістігінің ішкі жиынына дейінгі арақашықтық.
|
|
Н Гильберт кең істігі, М оның кейбір ішкі жиыны болсын.
 санын х элементінен М жиынына дейінгі арақ ашық тық дейді.
санын х элементінен М жиынына дейінгі арақ ашық тық дейді.
2-теорема. Н -Гильберт кең істігі, L оның кез-келген ішкең істігі болсын. Кез-келген 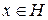 элементі ү шін L ішкең істігінің жалғ ыз y элементі табылып,
элементі ү шін L ішкең істігінің жалғ ыз y элементі табылып, 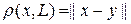 болады.
болады.
3-теорема. Н -Гильберт кең істігі, L оның кез-келген ішкі кең істігі болсын. Егер " 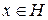 элементі ү шін $yÎ L,
элементі ү шін $yÎ L, 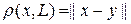 болса, онда
болса, онда
 болады.
болады.
2-мысал. 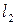 кең істігінің
кең істігінің 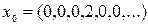 элементінен
элементінен 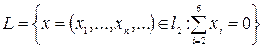 ішкең істігіне дейінгі арақ ашық тық ты табың ыз.
ішкең істігіне дейінгі арақ ашық тық ты табың ыз.
Шешуі. 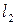 кең істігіне тиісті болғ ан
кең істігіне тиісті болғ ан 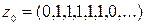 элементін қ арастырайық.Егер кейбір
элементін қ арастырайық.Егер кейбір  вектор L жиынына тиісті болса, онда
вектор L жиынына тиісті болса, онда
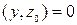 болуы қ ажет. Шынында да,
болуы қ ажет. Шынында да,
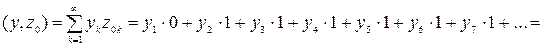

Демек,  векторының L жиынына тиісті болуы шарты
векторының L жиынына тиісті болуы шарты 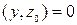 .Олай болса, z0 ^ L. Осы жерде L кең істігіне ортогонал болатын L ^ жиынында анық тап кетейік.Анық тама бойынша L ^={yÎ
.Олай болса, z0 ^ L. Осы жерде L кең істігіне ортогонал болатын L ^ жиынында анық тап кетейік.Анық тама бойынша L ^={yÎ 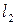 : " xÎ L: (x, y)=0 }.
: " xÎ L: (x, y)=0 }.
Бұ л жиын L ^={yÎ 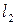 : y=a z0, aÎ R} болатыны айқ ын.
: y=a z0, aÎ R} болатыны айқ ын.
Лекция. Сызық тық оператор анық тамасы, ө зара бірмә нді, суперпозициялы операторлар. Сызық ты оператордың ү здіксіздігі, шенелгендігі, нормасы. Интегралды жә не дифференциал операторлар. Нормаланғ ан сызық ты операторлар кең істігі. Сызық ты жә не нормаланғ ан кең істіктегі кері операторлар
Н1 жә не Н2 – гильберт кең істіктері болсын делік. Егер барлық  ү шін
ү шін
 (1)
(1)
болса, онда Н1-ден Н2-ге дейін t операторы изометриялық деп аталады. Бұ л 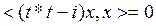 тең дігіне эквивалентті жә не сондық тан
тең дігіне эквивалентті жә не сондық тан
 (2)
(2)
болады. Бұ дан шығ атыны
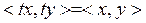 (барлық
(барлық 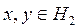 ү шін) (3)
ү шін) (3)
Егер t операторының бейнесі тұ тас Н2-мен бірдей болса, онда изометриялық оператор унитар оператор деп аталады. (1) шартынан t операторының ө зара бірмә нділігі шығ атындық тан Н1-дан Н2-ге деген унитар оператордың бар болуының қ ажетті жә не жеткілікті шарты болып Н1 мен Н2 кең істіктері ө лшемдерінің бірдейлігі табылады. Керісінше, егер 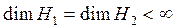 болса, онда Н1-ден Н2-ге деген кез келген изометриялық оператор унитар болады. Ақ ырсыз ө лшемді кең істіктер ү шін бұ л ұ йғ арым, ә рине, ә діл емес.
болса, онда Н1-ден Н2-ге деген кез келген изометриялық оператор унитар болады. Ақ ырсыз ө лшемді кең істіктер ү шін бұ л ұ йғ арым, ә рине, ә діл емес.
Гильберт кең істігі Н-тағ ы симметриялық жә не унитарлық операторлар нормальдық операторлардың дербес жағ дайы болып табылады. Егер t мен t* ауыстырымды болса
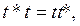 (4)
(4)
онда  операторы нормальдық деп аталады.
операторы нормальдық деп аталады.
Бұ л қ асиет келесіге эквивалентті:
барлық  ү шін
ү шін 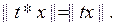 (5)
(5)
Нормальдық операторлардың маң ызды қ асиеті мынау:
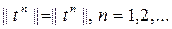 (6)
(6)
Бұ дан, жеке жағ дайда, спектралдық радиус
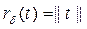 (7)
(7)
(6) формуланың дә лелдемесін біз симметриялық t операторының жеке жағ дайынан бастаймыз. Алдымен ескертеніміз
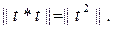 (8)
(8)
Расында да,  болатындық тан
болатындық тан
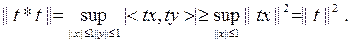
Басқ а жағ ынан, 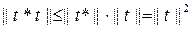 болатындық тан
болатындық тан 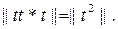 Осылайша,
Осылайша, 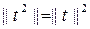 , t2 симметриялы болатындық тан
, t2 симметриялы болатындық тан 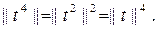 Осығ ан ұ қ сас пайымдап (6) тең дігі
Осығ ан ұ қ сас пайымдап (6) тең дігі 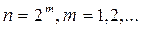 ү шін ә діл екенін кө реміз. t операторы нормальдық, бірақ міндетті тү рде симметриялық емес деп жориық. (8)-ді тағ ы қ олданып
ү шін ә діл екенін кө реміз. t операторы нормальдық, бірақ міндетті тү рде симметриялық емес деп жориық. (8)-ді тағ ы қ олданып  екенін аламыз. Бірақ (4) бойынша
екенін аламыз. Бірақ (4) бойынша 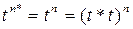 жә не
жә не 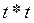 операторы симметриялық, онда
операторы симметриялық, онда 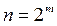 ү шін
ү шін 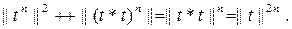 Осыдан (6)
Осыдан (6) 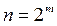 ү шін дә лелденді. Кез келген n жағ дайы ү шін
ү шін дә лелденді. Кез келген n жағ дайы ү шін 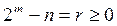 болатындай m-ді сайлаймыз. (6) формула
болатындай m-ді сайлаймыз. (6) формула 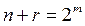 ү шін ә діл болатындық тан
ү шін ә діл болатындық тан 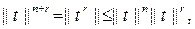 бұ дан
бұ дан  Қ арама-қ арсы тең сіздік айқ ын болғ ан себепті (6) тең дік дә лелденді.
Қ арама-қ арсы тең сіздік айқ ын болғ ан себепті (6) тең дік дә лелденді.
Симметриялық операторлардың маң ызды мысалы болып, ортогонал проектор немесе проекциялық оператор табылады. L H-кең істігінің кең істік асты болсын делік. Бенио Леви теоремасы бойынша кез келген  элементін
элементін 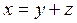 тү рінде бірмә нді кө рсетуге болады, мұ нда
тү рінде бірмә нді кө рсетуге болады, мұ нда 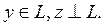
 деп тұ тас Н-та анық талғ ан мә ндерінің облысы L кең істік асты болатын кейбір операторды аламыз. Бұ л оператор проекциялық оператор (немесе L – кең істікастының ү стіне ортогонал проекциялау операторы) деп аталады жә не ол да
деп тұ тас Н-та анық талғ ан мә ндерінің облысы L кең істік асты болатын кейбір операторды аламыз. Бұ л оператор проекциялық оператор (немесе L – кең істікастының ү стіне ортогонал проекциялау операторы) деп аталады жә не ол да  деп белгіленеді.
деп белгіленеді.  операторы нормасы бірге тең ө зі тү йіндес оператор жә не
операторы нормасы бірге тең ө зі тү йіндес оператор жә не  шарты идемпотентті қ анағ аттандырады.
шарты идемпотентті қ анағ аттандырады.
Бә рінен бұ рын, π сызық тық оператор, із жү зінде, егер 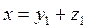 жә не
жә не  мұ нда
мұ нда 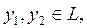 ал
ал 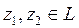 болса, онда
болса, онда 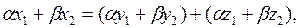 мұ нда
мұ нда  бұ дан
бұ дан 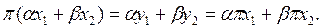 Ә рі қ арай у пен z-тің ортогоналдығ ынан,
Ә рі қ арай у пен z-тің ортогоналдығ ынан, 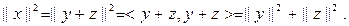 Сондық тан,
Сондық тан, 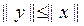 яғ ни кез келген х ү шін
яғ ни кез келген х ү шін  Бұ дан
Бұ дан 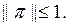
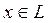 болғ андық тан
болғ андық тан 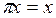 жә не сол себепті,
жә не сол себепті, 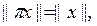 онда
онда 
π - ө зі тү йіндес оператор екенін кө рсетейік. х1 мен х2 тағ ы екі элемент, у1 пен у2 олардың L-дің ү стіне проекциясы болсын делік. 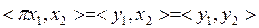 екенін аламыз. Осығ ан ұ қ сас,
екенін аламыз. Осығ ан ұ қ сас, 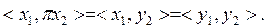 Сондық тан,
Сондық тан, 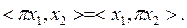 Ең соң ында, кез келген
Ең соң ында, кез келген  ү шін
ү шін 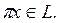 Сол себепті кез келген
Сол себепті кез келген  ү шін
ү шін 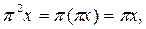 яғ ни
яғ ни 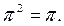
Кері ұ йғ арым да, анығ ында, кез келген ө зі тү йіндес идемпотенттік π операторы кейбір L кең істік ү стіне ортогонал проекциялау операторы екені де ә ділдігін кө рсетейік.  тү ріндегі элементтердің L жиынын қ арайық. Мұ нда х тұ тас Н-ты тү гендейді. π операторының аддитивтілігі мен біртектілігі бойынша жиыны сызық тық кө п бейне болады. L тұ йық екенін оң ай кө рсетуге болады. Іс жү зінде
тү ріндегі элементтердің L жиынын қ арайық. Мұ нда х тұ тас Н-ты тү гендейді. π операторының аддитивтілігі мен біртектілігі бойынша жиыны сызық тық кө п бейне болады. L тұ йық екенін оң ай кө рсетуге болады. Іс жү зінде 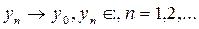 болсын делік.
болсын делік. 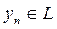 болғ андық тан кейбір
болғ андық тан кейбір 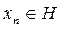 ү шін
ү шін 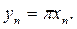 Сондық тан
Сондық тан 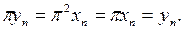 π операторының ү зіліссіздігі нә тижесінде,
π операторының ү зіліссіздігі нә тижесінде,  - ден
- ден 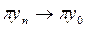 шығ ады.
шығ ады.  тең дігін ескеріп
тең дігін ескеріп 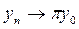 екенін аламыз. Сондық тан,
екенін аламыз. Сондық тан, 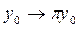 жә не
жә не 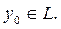
π операторының ө зі тү йіндестігі мен 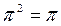 шартынан шығ атыны
шартынан шығ атыны 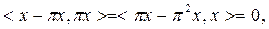 яғ ни
яғ ни  Енді L кең істікастының ө зінің анық тамасынан π осы кең істікасты ү стіне проекциялау операторы екені шығ ады жә не дә лелдеу керегі осы еді. L сондай, тек сондай,
Енді L кең істікастының ө зінің анық тамасынан π осы кең істікасты ү стіне проекциялау операторы екені шығ ады жә не дә лелдеу керегі осы еді. L сондай, тек сондай, 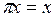 болатындай
болатындай 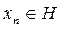 нү ктелерінен тұ ратынын ескертеміз.
нү ктелерінен тұ ратынын ескертеміз.
Дә лелденген, жеке жағ дайда, π мен бірге і-π -да проекциялық оператор екені шығ ады.
Проекциялық операторлардың кейбір қ арапайым қ асиеттерін атайық. Егер 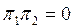 болса π 1 мен π 2 екі проекторы ортогонал деп аталады. Бұ л шарт
болса π 1 мен π 2 екі проекторы ортогонал деп аталады. Бұ л шарт 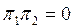 шартына пара-пар, себебі егер
шартына пара-пар, себебі егер 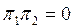 болса, онда
болса, онда 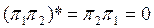 жә не керісінше.
жә не керісінше.
π 1 мен π 2 проекторлары ортогонал болуы ү шін сә йкес L1 жә не L2 кең ітік астылары ортогонал болуы қ ажетті жә не жеткілікті.
Іс жү зінде, егер 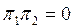 болса, онда
болса, онда 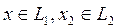 ү шін
ү шін
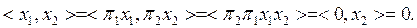
Керісінше, егер 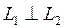 болса, онда кез келген
болса, онда кез келген  ү шін
ү шін 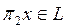 болады жә не сондық тан
болады жә не сондық тан 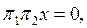 яғ ни
яғ ни 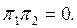
3-лемма. 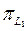 жә не
жә не 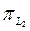 екі проекторының қ осындысы проектор болуы ү шін осы операторлардың ортогонал болуы қ ажетті жә не жеткілікті. Егер осы шарт орындалса, онда
екі проекторының қ осындысы проектор болуы ү шін осы операторлардың ортогонал болуы қ ажетті жә не жеткілікті. Егер осы шарт орындалса, онда  бұ дан
бұ дан 
Жеткіліктілігі  болсын делік. Сонда
болсын делік. Сонда 
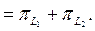 Сол себепті
Сол себепті  проекциялық оператор.
проекциялық оператор. 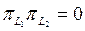 шарты бойынша L1 жә не L2 кең істікастылары ортогонал. Егер
шарты бойынша L1 жә не L2 кең істікастылары ортогонал. Егер  болса, онда
болса, онда
 (9)
(9)
Егер, ә рі қ арай, 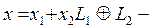 дегі элемент болса, онда
дегі элемент болса, онда 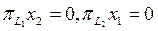 тең діктерін ескеріп, алатынымыз
тең діктерін ескеріп, алатынымыз

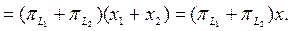 (10)
(10)
(9) бен (10) тең діктерінен π 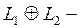 дің ү стіне проекциялық оператор екені шығ ады.
дің ү стіне проекциялық оператор екені шығ ады.
4-лемма. 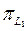 жә не
жә не 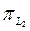 проекциялық екі оператордың кө бейтіндісі проекциялық оператор болуы ү шін
проекциялық екі оператордың кө бейтіндісі проекциялық оператор болуы ү шін 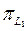 жә не
жә не 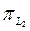 операторлары ауыстырымды болуы қ ажетті жә не жеткілікті. Егер осы шарт орындалса, онда
операторлары ауыстырымды болуы қ ажетті жә не жеткілікті. Егер осы шарт орындалса, онда 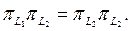
Дә лелдеме. Қ ажеттілігі.  ө зі тү йіндес оператор болса, онда
ө зі тү йіндес оператор болса, онда 
Жеткіліктігі. Егер 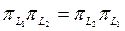 болса, онда
болса, онда  ө зі тү йіндес оператор. Сонымен қ атар,
ө зі тү йіндес оператор. Сонымен қ атар,
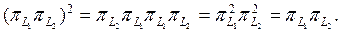
жә не сондық тан π – проекциялық оператор.
х Н-тағ ы кез келген элемент болсын делік. Сонда 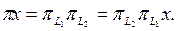 L1-ге де, L2-ге де, яғ ни
L1-ге де, L2-ге де, яғ ни 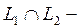 де жатады.
де жатады.
Енді 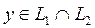 болсын делік. Сонда
болсын делік. Сонда 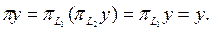 Осының бә рі π -
Осының бә рі π - 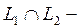 нің ү стіне проекциялық оператор екенін білдіреді.
нің ү стіне проекциялық оператор екенін білдіреді.
Егер 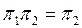 болса, онда проекциялық π 2 операторы проекциялық операторының бө лігі деп аталады. Тү йіндес операторғ а кө шу арқ ылы бұ л анық таманың
болса, онда проекциялық π 2 операторы проекциялық операторының бө лігі деп аталады. Тү йіндес операторғ а кө шу арқ ылы бұ л анық таманың 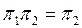 анық тамасына пара пар екеніне сенеміз. Анық тамадан тікелей шығ атыны
анық тамасына пара пар екеніне сенеміз. Анық тамадан тікелей шығ атыны 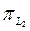 операторы
операторы 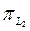 операторының сонда, тек сонда ғ ана бө лігі болады, егерде L2 кең істікасты L1 кең істікастынығ бө лігі болса ғ ана.
операторының сонда, тек сонда ғ ана бө лігі болады, егерде L2 кең істікасты L1 кең істікастынығ бө лігі болса ғ ана.
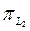 проекциялық операторы
проекциялық операторы 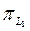 проекциялық операторының бө лігі болуына барлық
проекциялық операторының бө лігі болуына барлық  ү шін
ү шін 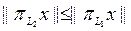 тең дігі орындалуы қ ажетті жә не жеткілікті.
тең дігі орындалуы қ ажетті жә не жеткілікті.
Іс жү зінде, 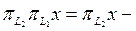 тен шығ атыны
тен шығ атыны 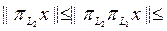
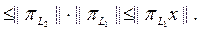 Керісінше, егер осы шарт орындалса, онда кез келген
Керісінше, егер осы шарт орындалса, онда кез келген 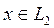 ү шін
ү шін 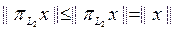 екенін аламыз жә не
екенін аламыз жә не  тең сіздігі де ә діл болатындық тан
тең сіздігі де ә діл болатындық тан  . Сол себепті, кез келген
. Сол себепті, кез келген  ү шін
ү шін  жә не, демек,
жә не, демек,  яғ ни
яғ ни 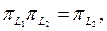 дә лелдеу керегі осы еді.
дә лелдеу керегі осы еді.
5-лемма. Екі проекциялық оператордың 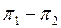 айырымы сонда, тек сонда ғ ана проекциялық болады, егер
айырымы сонда, тек сонда ғ ана проекциялық болады, егер 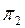
 дің бө лігі болса. Егер осы шарт орындалса, онда
дің бө лігі болса. Егер осы шарт орындалса, онда 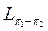
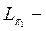 дегі
дегі  ге ортогонал толық тауыш болады.
ге ортогонал толық тауыш болады.
Дә лелдеме. Қ ажеттілігі. Егер 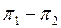 проекциялық оператор болса, онда
проекциялық оператор болса, онда 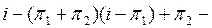 де проекциялық оператор. Бірақ онда 3-лемма бойынша
де проекциялық оператор. Бірақ онда 3-лемма бойынша 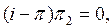 яғ ни
яғ ни 
Жеткіліктілігі. 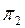
 дің бө лігі болсын. Сонда
дің бө лігі болсын. Сонда 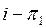 жә не
жә не 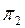 ортогонал, ә рі 3-лемма бойынша
ортогонал, ә рі 3-лемма бойынша 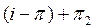 проекциялық оператор, жә не, содан,
проекциялық оператор, жә не, содан, 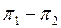 операторы да проекциялық.
операторы да проекциялық. 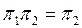 шартынан ең соң ында
шартынан ең соң ында 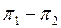 мен
мен 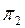 ортогонал екені шығ ады. Бірақ онда сол 3-лемма бойынша
ортогонал екені шығ ады. Бірақ онда сол 3-лемма бойынша