
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция. Түйіндес операторлар. Өз-өзіне түйіндес операторлар. Ортогонал проектрлеу операторы
|
|
Егер гильберт кең істігі Н-та анық талғ ан сызық тық операторларды қ арастырсақ, онда нақ ты жағ дайда Н пен Н/ бірдей болатындық тан жә не ондағ ы элементтердің скаляр кө бейтіндісі болатынын пайдаланып, айрық ша қ асиетті симметриясы бар (немесе) ө зі тү йіндестік қ асиеті деп аталатын операторлар класын ажыратуғ а болады жә не осы класстың операторларын еркін банах кең істігінде берілген еркін сызық тық операторларғ а қ арағ анда терең ірек зерттеу керек.
Н – комплекс гильберт кең істігі жә не t Н-та анық талғ ан жә не осы кең істіктегі мә ндерге ие болатын шектеулі сызық тық оператор болсын делік. Н-та берілген скаляр кө бейтінді бойынша t-ғ а тү йіндес t* операторын барлық  ү шін
ү шін
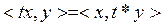 (1)
(1)
тең дігі бойынша анық таймыз.
1-анық тама. Сызық тық шектеулі t операторы егер
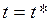 (2)
(2)
болса, онда шектеулі ө зі тү йіндес (немесе Эрмит симметриялы) оператор деп аталады.
Мысалдар. 1.  дегі ядросы
дегі ядросы  Фредгольм операторына тү йіндес оператор болып ядросы
Фредгольм операторына тү йіндес оператор болып ядросы  болатын Фредгольм операторы болып есептеледі. Ө зі тү йіндестік шартының тү рі
болатын Фредгольм операторы болып есептеледі. Ө зі тү йіндестік шартының тү рі  Нақ ты ядро жағ дайында бұ л шарт симметриялық шартына кө шеді.
Нақ ты ядро жағ дайында бұ л шарт симметриялық шартына кө шеді.
2.  дегі ә рбір
дегі ә рбір  функциясына
функциясына  функциясына сә йкес қ оятын t операторын қ ұ райық. Бұ л оператор ө зі тү йіндес екеніне кө з жеткізу қ иын емес.
функциясына сә йкес қ оятын t операторын қ ұ райық. Бұ л оператор ө зі тү йіндес екеніне кө з жеткізу қ иын емес.
Бұ дан ә рі «шектеулі» деген сө зді біз қ алдырып кетеміз. Алдың ғ ыдан, егер t - ө зі тү йіндес оператор жә не α -нақ ты сан болса, онда α t-да ө зі тү йіндес оператор, жә не егер t мен u - ө зі тү йіндес операторлар болса, онда u+t - ө зі тү йіндес, ал tu сонда, тек сонда ғ ана ө зі тү йіндес, егер t мен u операторы ауыстырымды болса. Ең соң ында, егер  бірқ алыпты немесе кү шті операорлық топология мағ ынасында жинақ ты болса, онда t-да ө зі тү йіндес оператор болады.
бірқ алыпты немесе кү шті операорлық топология мағ ынасында жинақ ты болса, онда t-да ө зі тү йіндес оператор болады.
Егер  ті х бойынша жә не у бойынша функционал болса, мұ нда t - ө зі тү йіндес оператор, онда біз
ті х бойынша жә не у бойынша функционал болса, мұ нда t - ө зі тү йіндес оператор, онда біз  деп белгілейтін осы функционал келесі шарттарды қ анағ аттандыратын кө ру қ иын емес:
деп белгілейтін осы функционал келесі шарттарды қ анағ аттандыратын кө ру қ иын емес:

Ондай функционалды біз бисызық ты Эрмит формасы деп атаймыз. Бұ л форма  мағ ынасында шектеулі, мұ нда Сt – кейбір тұ рақ ты (қ арастырғ ан жағ дайда
мағ ынасында шектеулі, мұ нда Сt – кейбір тұ рақ ты (қ арастырғ ан жағ дайда  ).
).
Сонымен, ә рбір ө зі тү йіндес t операторы кейбір шектеулі бисызық ты  Эрмит формасын тудырады.
Эрмит формасын тудырады.
Керісінше, егер шектеулі бисызық ты  Эрмит формасы берілсе, онда ол
Эрмит формасы берілсе, онда ол  тең дігін қ анағ аттандыратын кейбір ө зі тү йіндес t операторын тудырады.
тең дігін қ анағ аттандыратын кейбір ө зі тү йіндес t операторын тудырады.
Іс жү зінде, 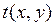 формасында у элементін белгілеп, біз х-тен сызық тық функционал аламыз. Сонымен
формасында у элементін белгілеп, біз х-тен сызық тық функционал аламыз. Сонымен  мұ нда у/ элементі бірмә нді анық талады. Сонда, біз
мұ нда у/ элементі бірмә нді анық талады. Сонда, біз 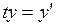 тең дігімен анық талатын жә не
тең дігімен анық талатын жә не  болатындай t операторын аламыз. t – сызық тық оператор екені айқ ын. t – шектеулі оператор екеніне оң ай кө з жеткізуге болады. Расында да
болатындай t операторын аламыз. t – сызық тық оператор екені айқ ын. t – шектеулі оператор екеніне оң ай кө з жеткізуге болады. Расында да
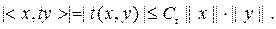
 деп жә не
деп жә не 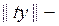 ке қ ысқ артып
ке қ ысқ артып  екенін табамыз. t - ө зі тү йіндес оператор екенін кө рсетеміз. Кез келген
екенін табамыз. t - ө зі тү йіндес оператор екенін кө рсетеміз. Кез келген  ү шін
ү шін 
 бұ дан
бұ дан 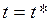 жә не
жә не  екені шығ ады.
екені шығ ады.
Енді бисызық ты 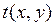 Эрмит формасын аламыз жә не онда
Эрмит формасын аламыз жә не онда 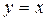 делік. Барлық х-тер ү шін нақ ты мә ндер алып
делік. Барлық х-тер ү шін нақ ты мә ндер алып
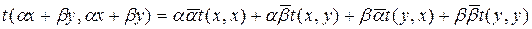
болатындай 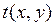 квадрат формасын аламыз. Сондай
квадрат формасын аламыз. Сондай  формасын
формасын 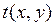 бисызық ты Эрмит формасына сә йкес квадраттық Эрмит формасы деп атаймыз. Егер
бисызық ты Эрмит формасына сә йкес квадраттық Эрмит формасы деп атаймыз. Егер 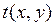 бисызық ты Эрмит формасы берілсе, онда сол арқ ылы сә йкес квадраттық
бисызық ты Эрмит формасы берілсе, онда сол арқ ылы сә йкес квадраттық  Эрмит формасы беріледі. Кері жағ дай да ақ иқ ат, квдарттық
Эрмит формасы беріледі. Кері жағ дай да ақ иқ ат, квдарттық  Эрмит формасы берілуі бисызық ты
Эрмит формасы берілуі бисызық ты 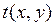 Эрмит формасын бірмә нді анық тайды. Бұ л бисызық ты форма келесі тең дікпен анық талады (полярлау принципі)
Эрмит формасын бірмә нді анық тайды. Бұ л бисызық ты форма келесі тең дікпен анық талады (полярлау принципі)
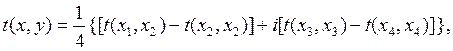 (3)
(3)
мұ нда  жә не
жә не 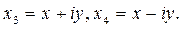
Квадраттық Эрмит формасы  сонда, тек сонда ғ ана шектеулі болады, яғ ни
сонда, тек сонда ғ ана шектеулі болады, яғ ни 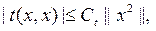 егер сә йкес бисызық ты форма шектеулі болса ғ ана екенін кө рсету қ иын емес.
егер сә йкес бисызық ты форма шектеулі болса ғ ана екенін кө рсету қ иын емес. 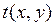 формасы
формасы  ү шін полярлық деп аталады.
ү шін полярлық деп аталады.

болсын делік.
m жә не М сандары ө зі тү йіндес t операторының тө менгі жә не жоғ арғ ы шекарасы деп аталады.
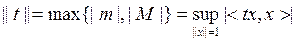
екенін кө рсетейік.
Іс жү зінде,  болсын делік. Сонда
болсын делік. Сонда
 (4)
(4)
жә не сондық тан 
Басқ а жағ ынан, кез келген  ү шін
ү шін  болады. Сондық тан, егер z Н-тағ ы нө лден ерекше элемент болса, онда
болады. Сондық тан, егер z Н-тағ ы нө лден ерекше элемент болса, онда

деп 
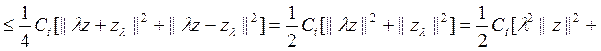
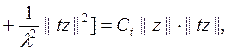
екенін аламыз, бұ дан 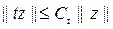 жә не содан
жә не содан
 (5)
(5)
(4) жә не (5) тең сіздіктерінен керекті тең дікті аламыз. Дә лелденген бойынша, жеке жағ дайда, егер барлық  ү шін ө зі тү йіндес t мен u операторлары
ү шін ө зі тү йіндес t мен u операторлары  тең дігі орындалса, онда
тең дігі орындалса, онда 
Лекция. Сызық ты оператордың меншікті мә ндері мен меншікті векторлары. Ә сіре ү зіліссіз оператордың меншікті мә ндері мен меншікті векторлары
Е – сызық тық кең істік жә не t Е-де ә сер ететін, анық талу облысы D(t) болатын сызық тық оператор болсын делік.
1-АНЫҚ ТАМА. Егер
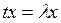 (1)
(1)
болатындай  векторы бар болса, онда λ t-операторының меншікті мә ні деп аталады. Мұ нда х векторы меншікті λ мә ніне сә йкес t операторының меншікті векторы деп аталады.
векторы бар болса, онда λ t-операторының меншікті мә ні деп аталады. Мұ нда х векторы меншікті λ мә ніне сә йкес t операторының меншікті векторы деп аталады.
1-тұ жырым. Сызық тық операторлардың ә ртү рлі меншікті мә ндеріне жауап беретін меншікті векторлар сызық ты тә уелсіз.
Дә лелдеме. Сызық тық операторлардың меншікті λ 1 мә ніне жауап беретін сызық тық операторлардың бір меншікті х1 векторы сызық ты тә уелсіз, себебі 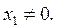 Дә лелдеуді индукция бойынша жү ргіземіз t операторының ә ртү рлі меншікті мә ндеріне сә йкес кез келген k меншікті векторлары сызық ты тә уелсіз болсын делік. Сонда да, егер
Дә лелдеуді индукция бойынша жү ргіземіз t операторының ә ртү рлі меншікті мә ндеріне сә йкес кез келген k меншікті векторлары сызық ты тә уелсіз болсын делік. Сонда да, егер  болса,
болса,  болатын меншікті
болатын меншікті  мә ндеріне жауап беретін меншікті
мә ндеріне жауап беретін меншікті 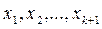
 векторлары сызық ты тә уелді деп жориық. Онда, нө лге біруақ ытта тең болмайтын жә не
векторлары сызық ты тә уелді деп жориық. Онда, нө лге біруақ ытта тең болмайтын жә не
 (2)
(2)
болатындай  скалярлары табылады. Бұ л тең дікке
скалярлары табылады. Бұ л тең дікке 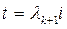 операторын қ олдана отырып
операторын қ олдана отырып 

екенін аламыз. Бірақ  индукциялық жору бойынша сызық ты тә уелсіз жә не сондық тан
индукциялық жору бойынша сызық ты тә уелсіз жә не сондық тан
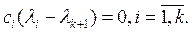
Бұ дан 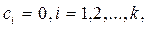 себебі
себебі 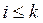 ү шін
ү шін 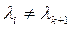 (2) бойынша
(2) бойынша  Бұ л барлық сі біруақ ытта нө лге тең емес дегенімізге қ айшы. Сондық тан
Бұ л барлық сі біруақ ытта нө лге тең емес дегенімізге қ айшы. Сондық тан  -дің сызық ты тә уелділігі туралы жоруымыз дұ рыс емес. Теорема дә лелденді.
-дің сызық ты тә уелділігі туралы жоруымыз дұ рыс емес. Теорема дә лелденді.
Лекция. Сызық ты оператордың спектрі жә не резольвенттік жиын ұ ғ ымдары, мысалдар. Резольвента аналитикалық оператор- функция ретінде. Стильтес интегралы жә не шенелген вариацияның абстракты функциялары
2-АНЫҚ ТАМА. Егер  ү шін мә ндер облысы
ү шін мә ндер облысы  -кең істігінде тығ ыз жә не
-кең істігінде тығ ыз жә не  операторының ү зілісіз кері операторы
операторының ү зілісіз кері операторы  бар болса, онда комплекс λ 0 саны t операторының резольвенттік
бар болса, онда комплекс λ 0 саны t операторының резольвенттік  жиынында жатады дейміз.
жиынында жатады дейміз.
 операторын біз
операторын біз  деп белгілеп, t операторының
деп белгілеп, t операторының  нү ктесіндегі резольвентасы деп атаймыз. Резольвенттік
нү ктесіндегі резольвентасы деп атаймыз. Резольвенттік  жиынына жатпайтын барлық комплекс λ сандарының жиынтығ ы t операторының спектрі деп аталады. Бұ л жиынды біз
жиынына жатпайтын барлық комплекс λ сандарының жиынтығ ы t операторының спектрі деп аталады. Бұ л жиынды біз  деп белгілейміз.
деп белгілейміз.  спектрін қ ос-қ осымен қ иылыспайтындай, келесі қ асиеттерді қ анағ аттандыратын,
спектрін қ ос-қ осымен қ иылыспайтындай, келесі қ асиеттерді қ анағ аттандыратын, 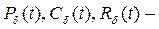 ү ш жиынғ а ажыратуғ а болады.
ү ш жиынғ а ажыратуғ а болады.
 операторының керісі болмайтындай комплекс сандарының жиыны,
операторының керісі болмайтындай комплекс сандарының жиыны, 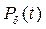 t – операторының нү ктелік спектрі деп аталады.
t – операторының нү ктелік спектрі деп аталады.
 операторының анық талу облысы Е-де тығ ыз кері операторы болатындай (
операторының анық талу облысы Е-де тығ ыз кері операторы болатындай ( операторы ү зіліссіз емес) комплекс λ сандарының жиыны,
операторы ү зіліссіз емес) комплекс λ сандарының жиыны,  t – операторының ү зіліссіз спектрі деп аталады.
t – операторының ү зіліссіз спектрі деп аталады.
 ның анық талу облысы Е-де тығ ыз емес болатын кері операторы бар болатындай комплекс λ сандарының жиыны,
ның анық талу облысы Е-де тығ ыз емес болатын кері операторы бар болатындай комплекс λ сандарының жиыны,  операторының қ алдық спектрі деп аталады.
операторының қ алдық спектрі деп аталады.
1 жә не 2-анық тамалардан t операторының сызық тылығ ын ескере отырып, келесі ұ йғ арымдарды қ орытамыз.
2-тұ жырым.  ү шін
ү шін 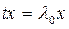 тең деуінің нө лден ерекше
тең деуінің нө лден ерекше 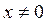 шешімі болуы қ ажетті жә не жеткілікті.
шешімі болуы қ ажетті жә не жеткілікті.
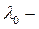 ге сә йкес меншікті кең істік астының ө лшемі меншікті
ге сә йкес меншікті кең істік астының ө лшемі меншікті 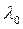 мә нінің еселігі деп аталады.
мә нінің еселігі деп аталады.
2-ТЕОРЕМА. Е комплекс банах кең істігі жә не t анық талу облысы мен мә ндерінің облысы Е-де жататын тұ йық, сызық тық оператор болсын делік. Сонда кез келген 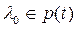 ү шін
ү шін  резольвентасы тұ тас Е кең істігінде анық талғ ан ү зіліссіз сызық тық операторды кө рсетеді.
резольвентасы тұ тас Е кең істігінде анық талғ ан ү зіліссіз сызық тық операторды кө рсетеді.
Дә лелдеме. 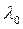 резольвенттік
резольвенттік  жиында жататындық тан,
жиында жататындық тан, 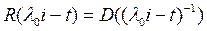 жиыны Е-де тығ ыз, ә рі
жиыны Е-де тығ ыз, ә рі

болатындай тұ рақ ты с саны бар болады.
Біз 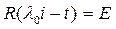 болатынын кө рсетуіміз керек. Кейбір
болатынын кө рсетуіміз керек. Кейбір  тізбегі ү шін
тізбегі ү шін  шегі бар деп жориық. Сонда жоғ арыдағ ы тең сіздіктен
шегі бар деп жориық. Сонда жоғ арыдағ ы тең сіздіктен 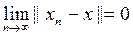 шегі де бар болады. t операторы тұ йық болғ андық тан
шегі де бар болады. t операторы тұ йық болғ андық тан  Сондық тан,
Сондық тан, 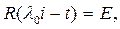 ө йткені теореманың ұ йғ арымы бойынша
ө йткені теореманың ұ йғ арымы бойынша 
3-ТЕОРЕМА. Егер λ жә не 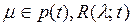 мен
мен  операторлары тұ тас Е кең істігінде анық талғ ан жә не ү зіліссіз болса, онда кейде резольвенттік тең деу деп аталатын гильберт тепе-тең дігі
операторлары тұ тас Е кең істігінде анық талғ ан жә не ү зіліссіз болса, онда кейде резольвенттік тең деу деп аталатын гильберт тепе-тең дігі
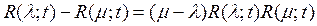 (2)
(2)
ә діл.
Дә лелдеме. Тікелей есептеуден шығ атыны 
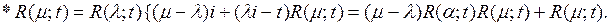
4-ТЕОРЕМА. (И.М.Гельфанд). Егер шектеулі сызық тық t операторы комплекс банах кең істігі Е-ні ө зіне бейнелесе, онда
 (3)
(3)
шегі бар болады. 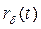 шегі t операторының спектралдық радиусы деп аталады, ол ү шін мына бағ а ә діл:
шегі t операторының спектралдық радиусы деп аталады, ол ү шін мына бағ а ә діл:
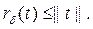 (4)
(4)
Егер  болса, онда
болса, онда  резольвентасы бар болады жә не операторлар нормасы бойынша жинақ талатын
резольвентасы бар болады жә не операторлар нормасы бойынша жинақ талатын
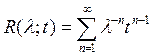 (5)
(5)
қ атары тү рінде кө рсетіледі.
Дә лелдеме.  делік.
делік.

екенін кө рсету жеткілікті.
Ә рбір  ү шін
ү шін  болатындай бү тін оң m санын таң даймыз. Сонан соң, еркін k бү тін саны ү шін 2 арқ ылы
болатындай бү тін оң m санын таң даймыз. Сонан соң, еркін k бү тін саны ү шін 2 арқ ылы 
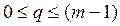 (р – бү тін)-ді қ анағ аттандыратын мә нді белгілейміз. Сонда
(р – бү тін)-ді қ анағ аттандыратын мә нді белгілейміз. Сонда 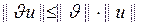 тең сіздігін пайдаланып, біз
тең сіздігін пайдаланып, біз

екенін аламыз, 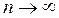 ү шін
ү шін  жә не
жә не  болатындық тан
болатындық тан

екені шығ ады. Бұ дан  болғ анда (5) қ атар операторлар нормасы бойынша жинақ талады. Іс жү зінде, егер
болғ анда (5) қ атар операторлар нормасы бойынша жинақ талады. Іс жү зінде, егер 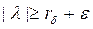 болса, мұ нда
болса, мұ нда  онда (3) бойынша кез келген жеткілікті мө лшерде ү лкен n ү шін
онда (3) бойынша кез келген жеткілікті мө лшерде ү лкен n ү шін 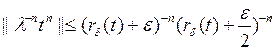 болады, бұ дан (5) қ атар жинақ ты екені кө рінеді. Бұ л қ атарды сол жә не оң жақ тан
болады, бұ дан (5) қ атар жинақ ты екені кө рінеді. Бұ л қ атарды сол жә не оң жақ тан  ғ а кө бейтіп, біз тепе-тең і операторын аламыз, сондық тан
ғ а кө бейтіп, біз тепе-тең і операторын аламыз, сондық тан  резольвентасы расында (5) қ атармен кө рсетіледі.
резольвентасы расында (5) қ атармен кө рсетіледі.
Салдар. Кез келген шектеулі сызық тық, банах кең істігі Е-ні ө зіне бейнелейтін t операторы ү шін резольвенттік p(t) жиыны бос емес.
5-ТЕОРЕМА. t Е-дегі толығ ымен ү зіліссіз оператор болсын делік. Сонда кез келген  ү шін комплекс жазық тық тағ ы (нақ ты осьтегі)
ү шін комплекс жазық тық тағ ы (нақ ты осьтегі)  дө ң гелегенінен тысқ ары t операторының тек ақ ырлы санды меншікті мә ндері жатады.
дө ң гелегенінен тысқ ары t операторының тек ақ ырлы санды меншікті мә ндері жатады.
Дә лелдеме. Кері жориық,  , бірақ t-ның ә ртү рлі меншікті мә ндерінің
, бірақ t-ның ә ртү рлі меншікті мә ндерінің 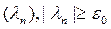 тізбегі болатындай
тізбегі болатындай 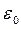 табылады делік. 1-тұ жырым бойынша
табылады делік. 1-тұ жырым бойынша  сызық ты тә уелсіз.
сызық ты тә уелсіз.
Е-дегі 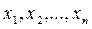 -ге керілген Еn ең істік астын енгіземіз.
-ге керілген Еn ең істік астын енгіземіз.

екені айқ ын, ә рі ешбір n ү шін  емес. Барлық Еn ақ ырлы ө лшемді жә не сондық тан тұ йық. Перпендикуляр дерлік туралы Рисс теоремасы, 6-лемме, 5-тар бойынша барлық
емес. Барлық Еn ақ ырлы ө лшемді жә не сондық тан тұ йық. Перпендикуляр дерлік туралы Рисс теоремасы, 6-лемме, 5-тар бойынша барлық  ү шін
ү шін 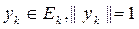 жә не
жә не 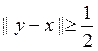 болатындай
болатындай  векторлар тізбегі табылады.
векторлар тізбегі табылады.
 ді қ арайық.
ді қ арайық.  шектеулі болғ андық тан t толығ ымен ү зіліссіз, онда
шектеулі болғ андық тан t толығ ымен ү зіліссіз, онда  компактылы. Келесі пайымдаулар
компактылы. Келесі пайымдаулар  компактылы болуы мү мкін еместігін кө рсетеді, демек, біздің меншікті мә ндердің ақ ырсыз тізбегі болады деп жоруымыз дұ рыс емес, бұ дан дә лелденіп отырғ ан теореманың ә ділдігі шығ ады.
компактылы болуы мү мкін еместігін кө рсетеді, демек, біздің меншікті мә ндердің ақ ырсыз тізбегі болады деп жоруымыз дұ рыс емес, бұ дан дә лелденіп отырғ ан теореманың ә ділдігі шығ ады.
Сонымен,  нің компактылы емес екенін кө рсету қ алды.
нің компактылы емес екенін кө рсету қ алды.  белгілеуін енгіземіз. Кез келген
белгілеуін енгіземіз. Кез келген  ү шін
ү шін


екенін аламыз, мұ нда қ абылданғ ан 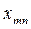 белгілеуі айқ ын. Егер
белгілеуі айқ ын. Егер 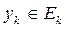 болса, онда
болса, онда 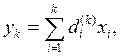 себебі
себебі 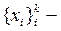 дағ ы базис. Сол себепті
дағ ы базис. Сол себепті

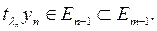
Сонымен,  бірақ онда
бірақ онда  жә не сондық тан
жә не сондық тан

Бұ дан  нің компактылы еместігі шығ ады, с.т.р.
нің компактылы еместігі шығ ады, с.т.р.
Лекция. Ө з-ө зіне тү йіндес оператордың спектралды функциялары. Кез келген ө з-ө зіне тү йіндес оператордың спектралды функциясының бар болуы. Шенелмеген ө з-ө зіне тү йіндес оператордың спектралды жіктеуі
 операторларының ү йірін қ арайық, мұ нда t ө зі тү йіндес оператор жә не λ – комплекс сан.
операторларының ү йірін қ арайық, мұ нда t ө зі тү йіндес оператор жә не λ – комплекс сан.
2-тұ жырымнан, егер 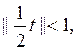 яғ ни егер
яғ ни егер 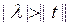 болса, онда λ t-операторының регуляр мә ні жә не, сондық тан, t операторының барлық спектрі
болса, онда λ t-операторының регуляр мә ні жә не, сондық тан, t операторының барлық спектрі 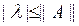 дө ң гелегінің ішінде не шекарасында жатады. Бұ л банах кең істігінде ә сер ететін кез келген сызық тық оператор ү шін ә діл. Гильберт кең істігінде берілген ө зі тү йіндес оператор жағ дайында біз тө менде оператордың спектрі орналасатын облысты дә лірек анық таймыз.
дө ң гелегінің ішінде не шекарасында жатады. Бұ л банах кең істігінде ә сер ететін кез келген сызық тық оператор ү шін ә діл. Гильберт кең істігінде берілген ө зі тү йіндес оператор жағ дайында біз тө менде оператордың спектрі орналасатын облысты дә лірек анық таймыз.
Егер t ө зі тү йіндес оператор болса, онда оның барлық меншікті мә ндері нақ ты, себебі 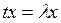 тең дігінен
тең дігінен  екені шығ ады, мұ ндағ ы екі скаляр кө бейтінді
екені шығ ады, мұ ндағ ы екі скаляр кө бейтінді  мен
мен 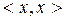 нақ ты. Ә рі қ арай,
нақ ты. Ә рі қ арай, 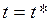 шартынан, меншікті мә ндердің нақ тылығ ынан жә не t мен t*-ның ә ртү рлі меншікті мә ндеріне ортогонал меншікті векторлар сә йкес келетіндігін ө зі тү йіндес оператордың ә ртү рлі меншікті мә ндеріне сә йкес келетін меншікті элементтер ортогонал екені шығ ады.
шартынан, меншікті мә ндердің нақ тылығ ынан жә не t мен t*-ның ә ртү рлі меншікті мә ндеріне ортогонал меншікті векторлар сә йкес келетіндігін ө зі тү йіндес оператордың ә ртү рлі меншікті мә ндеріне сә йкес келетін меншікті элементтер ортогонал екені шығ ады.
10-теорема. λ нү ктесі ө зі тү йіндес t операторының регуляр мә ні болуы ү шін кез келген  ү шін
ү шін
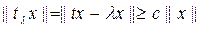 (1)
(1)
болатындай тұ рақ ты оң С санының бар болуы қ ажетті жә не жеткілікті.
Дә лелдеме. Қ ажеттілігі. Шектеулі 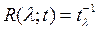 жә не
жә не 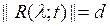 операторы бар болсын делік. Кез келген
операторы бар болсын делік. Кез келген  ү шін
ү шін 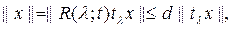 яғ ни
яғ ни  жә не қ ажеттілігі дә лелденді.
жә не қ ажеттілігі дә лелденді.
Жеткіліктілігі. 1-тұ жырымнан шығ ады.
Салдар. λ нү ктесі ө зі тү йіндес t операторының спектрінде сонда, тек сонда ғ ана жатады, егер
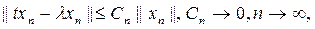 (2)
(2)
болатындай 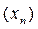 тізбегі бар болса.
тізбегі бар болса.
(2) тең сіздігінде  деуге болады, сонда
деуге болады, сонда
 (3)
(3)
11-теорема.  комплекс сандары ө зі тү йіндес t операторының регулятор мә ндері болады.
комплекс сандары ө зі тү йіндес t операторының регулятор мә ндері болады.
Дә лелдеме. Іс жү зінде, егер  болса, онда
болса, онда 
 Бұ дан
Бұ дан 
немесе

жә не, демек,
 яғ ни
яғ ни  (4)
(4)
Сондық тан 10-теорема бойынша осы теореманың да дә ледемесі шығ ады.
12-теорема. Ө зі тү йіндес t операторының спектрі сан осінің  кесіндісіне жатады, мұ нда
кесіндісіне жатады, мұ нда
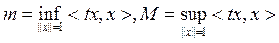
Дә лелдеу барысында теоремадан спектр тек нақ ты осьте ғ ана жата алады.  кесіндісінен тысқ ары жатқ ан нақ ты λ -лар регуляр мә ндер болатынын кө рсетейік. Мысалғ а,
кесіндісінен тысқ ары жатқ ан нақ ты λ -лар регуляр мә ндер болатынын кө рсетейік. Мысалғ а,  болсын делік.
болсын делік. 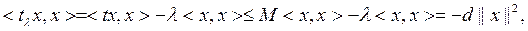 яғ ни
яғ ни 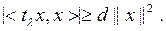 Басқ а жағ ынан,
Басқ а жағ ынан, 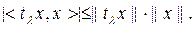 Сондық тан,
Сондық тан,  Бұ дан 10-теорема бойынша, λ мә ндерінің регулярлығ ы шығ ады.
Бұ дан 10-теорема бойынша, λ мә ндерінің регулярлығ ы шығ ады.
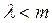 жағ дайы осығ ан ұ қ сас қ арастырылады.
жағ дайы осығ ан ұ қ сас қ арастырылады.
13-теорема. Мысалғ а, М ү шін дә лелдейік. Егер t операторын  операторына алмастырсақ, онда спектр солғ а қ арай μ -ге жылжиды, ал М жә не m саны М-μ мен m-μ –ге алмасатынын байқ аймыз. Біз, пайымдаудың жалпылығ ын тө мендетпей,
операторына алмастырсақ, онда спектр солғ а қ арай μ -ге жылжиды, ал М жә не m саны М-μ мен m-μ –ге алмасатынын байқ аймыз. Біз, пайымдаудың жалпылығ ын тө мендетпей,  деп санай аламыз. Бұ л жағ дайда, §3-тің соң ында кө рсетілгендей
деп санай аламыз. Бұ л жағ дайда, §3-тің соң ында кө рсетілгендей  М – спектрдің нү ктесі екенін дә лелдейік.
М – спектрдің нү ктесі екенін дә лелдейік.
Іс жү зінде,  санының анық тамасынан
санының анық тамасынан 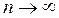 ү шін
ү шін  болатындай
болатындай  элементтерінің тізбегі бар болады. Ә рі қ арай,
элементтерінің тізбегі бар болады. Ә рі қ арай, 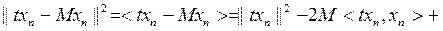
 немесе
немесе  Сонымен,
Сонымен, 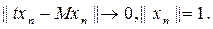 Сондық тан, 10-теореманың салдарынан М саны t операторының спектрінде жатады. Осығ ан ұ қ сас, m t-операторының спектріне жататыны дә лелденді.
Сондық тан, 10-теореманың салдарынан М саны t операторының спектрінде жатады. Осығ ан ұ қ сас, m t-операторының спектріне жататыны дә лелденді.
Салдар. Ә рбір ө зі тү йіндес оператордың бос емес спектрі бар.
Егер 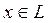 -ден
-ден  шығ атын болса, онда Н кең істігінің t операторының инвариант кең істікасты деп аталады. Инвариант кең істікастының мысалын келтірейік. λ t-операторының меншікті мә ні жә не Nλ осы меншікті мә нге сә йкес, нө л элементі қ осылғ ан, меншікті элементтердің жиынтығ ы болсын делік.
шығ атын болса, онда Н кең істігінің t операторының инвариант кең істікасты деп аталады. Инвариант кең істікастының мысалын келтірейік. λ t-операторының меншікті мә ні жә не Nλ осы меншікті мә нге сә йкес, нө л элементі қ осылғ ан, меншікті элементтердің жиынтығ ы болсын делік. 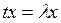 тең дігі бойынша
тең дігі бойынша 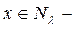 дан
дан  шығ атындық тан Nλ –инвариант кең істікасты болады.
шығ атындық тан Nλ –инвариант кең істікасты болады.
Егер L t – операторының инвариант кең істікасты болса, онда L е-ны жетектейді дейді. Ө зі тү йіндес операторлардың инвариант кең істерінің қ асиеттерін келтірейік.
3-тұ жырым. L-дің инварианттылығ ынан оның ортогонал  толық тауышының да инварианттығ ы шығ ады.
толық тауышының да инварианттығ ы шығ ады.
Дә лелдеме. 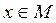 болсын делік. Бұ л кез келген
болсын делік. Бұ л кез келген 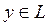 ү шін
ү шін  екенін білдіреді. Бірақ
екенін білдіреді. Бірақ 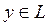 ү шін
ү шін  те L-де жатады, сондық тан
те L-де жатады, сондық тан  Бұ дан t-ның ө зі тү йіндестігінен кез келген
Бұ дан t-ның ө зі тү йіндестігінен кез келген 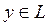 ү шін
ү шін  екенін аламыз. Содан,
екенін аламыз. Содан,  Сλ арқ ылы tλ операторы мә ндерінің облысын белгілейміз, яғ ни
Сλ арқ ылы tλ операторы мә ндерінің облысын белгілейміз, яғ ни  тү ріндегі элементтердің жиынтығ ы, мұ нда λ – меншікті мә н.
тү ріндегі элементтердің жиынтығ ы, мұ нда λ – меншікті мә н.
4-тұ жырым. t операторы мә ндерінің  облысының
облысының 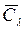 тұ йық тамасы ө зі тү йіндес t операторының инвариант кең істікасты болады.
тұ йық тамасы ө зі тү йіндес t операторының инвариант кең істікасты болады.
Дә лелдеме. 3-тұ джырым бойынша ұ йғ арымды дә лелдеу ү шін 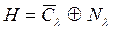 екенін дә лелдеу жеткілікті. Соң ғ ы жағ дай келесі пайымдаулардан шығ ады. Кез келген
екенін дә лелдеу жеткілікті. Соң ғ ы жағ дай келесі пайымдаулардан шығ ады. Кез келген  жә не
жә не  ү шін
ү шін 
Сондық тан,  Егер
Егер  жә не
жә не  болса, онда
болса, онда  мұ нда
мұ нда  .
. 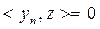 тең дігінен
тең дігінен 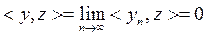 екенін аламыз. Сондық тан
екенін аламыз. Сондық тан  Енді кез келген
Енді кез келген  ү шін
ү шін  екенін аламыз, бұ дан
екенін аламыз, бұ дан  яғ ни
яғ ни 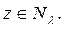 Сондық тан,
Сондық тан, 
N арқ ылы барлық Nλ кең істікастыларының ортогонал қ осындысын немесе соғ ан пара-пар t операторының барлық меншікті элементтерінің тұ йық сызық тық қ абығ ын белгілейміз. Егер Н сепарабелді болса, онда ә рбір Nλ –да меншікті мә ндердің ақ ырлы немесе санақ ты ортонормаланғ ан толық системасын қ ұ руғ а болады. Ә ртү рлі Nλ -дағ ы меншікті элементтер ортогонал болатындық тан, онда осы системаларды біріктіріп біз тағ ы да N-кең істігінде толық, меншікті  элементтерінің ортонормаль системасын аламыз.
элементтерінің ортонормаль системасын аламыз.
t операторы инвариант L кең істікастында 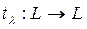 операторын анық тайды, атап айтқ анда,
операторын анық тайды, атап айтқ анда, 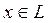 ү шін
ү шін 
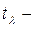 дағ ы ө зі тү йіндес оператор екенін тексеру қ иын емес.
дағ ы ө зі тү йіндес оператор екенін тексеру қ иын емес.
5-тұ жырым. Егер инвариант L жә не М кең істікастылары ө зді-ө зіне ортогонал толық тауыштар қ ұ раса, онда t операторының спектрі  мен
мен  операторының жиындық -теориялық қ осындысы анық талады.
операторының жиындық -теориялық қ осындысы анық талады.
Дә лелдеме. λ 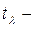 немесе
немесе  операторының спектр нү ктесі болсын делік. Сонда
операторының спектр нү ктесі болсын делік. Сонда  болатындай
болатындай  элементтерінің тізбегі бар болады. Бірақ
элементтерінің тізбегі бар болады. Бірақ  сондық тан λ t-операторының спектріне жатады.
сондық тан λ t-операторының спектріне жатады.
Енді λ  операторының да,
операторының да,  операторының да спектріне жатпасын делік. Сонда кез келген
операторының да спектріне жатпасын делік. Сонда кез келген  жә не
жә не  ү шін
ү шін
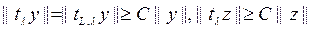
болатындай оң сан бар болады. Бірақ кез келген  элементі
элементі  тү рінде болады. Бұ дан
тү рінде болады. Бұ дан

Сонымен, λ спектр нү ктесі емес.
Сонымен, біз Н кең істігін екі кең істіктің: ө зі тү йіндес t операторының барлық меншікті векторлар жиынының тұ йық сызық тық қ абығ ының N кең істігі мен оның ортогонал С толық тауышының ортогонал қ осындысы деп кө рсетуге болатынын кө реміз. N кең істігі операторының инвариант кең істікасты болады, демек t операторының спектрі 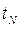 жә не
жә не  операторлары спектрлерінің жиындық -теориялық қ осындысы болады.
операторлары спектрлерінің жиындық -теориялық қ осындысы болады. 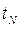 операторының спектрі t операторының нү ктелік спектрі деп аталады.
операторының спектрі t операторының нү ктелік спектрі деп аталады.  операторының спектрі t операторының ү зіліссіз спектрі деп аталады. Егер M=N болса, онда ү зіліссіз спектр болмайды жә не t операторының мү лдем нү ктелік спектрі болады, ондай спектрдің толығ ымен ү зіліссіз операторы болады. Егер оператордың меншікті элементтері болмаса, онда N кең істікасты бос, H=C жә не t операторының спектрі мү лдем ү зіліссіз.
операторының спектрі t операторының ү зіліссіз спектрі деп аталады. Егер M=N болса, онда ү зіліссіз спектр болмайды жә не t операторының мү лдем нү ктелік спектрі болады, ондай спектрдің толығ ымен ү зіліссіз операторы болады. Егер оператордың меншікті элементтері болмаса, онда N кең істікасты бос, H=C жә не t операторының спектрі мү лдем ү зіліссіз.
Егер t операторының мү лдем нү ктелік спектрі болса жә не  меншікті λ n мә ндеріне сә йкес, меншікті элементтердің ортонормаль системасы болса, онда
меншікті λ n мә ндеріне сә йкес, меншікті элементтердің ортонормаль системасы болса, онда
 (5)
(5)
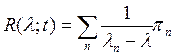 (6)
(6)
екенін дә лелдеуге болады, мұ нда π n  тең дігімен анық талатын проекциялық оператор.
тең дігімен анық талатын проекциялық оператор.
14-теорема. Егер  t-операторының спектр нү ктесі болса, онда
t-операторының спектр нү ктесі болса, онда  болатындай
болатындай 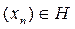 элементтердің тізбегі бар болады, бұ дан
элементтердің тізбегі бар болады, бұ дан  деп
деп 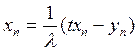 екенін аламыз. t операторы
екенін аламыз. t операторы 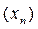 тізбегін компактылы
тізбегін компактылы 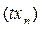 тізбегіне тү рлендіреді. Сондық тан жинақ ты
тізбегіне тү рлендіреді. Сондық тан жинақ ты 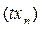 тізбегі бар болады, сонымен қ атар
тізбегі бар болады, сонымен қ атар
 (7)
(7)
тізбегі де жинақ талады.  болсын делік. Сонда
болсын делік. Сонда 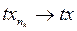 болады, ә рі қ арай,
болады, ә рі қ арай,  сондық тан (7) тең діктен
сондық тан (7) тең діктен  немесе
немесе 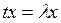 екені шығ ады. Онда
екені шығ ады. Онда  Сондық тан, х – меншікті вектор, ал λ t – операторының меншікті мә ні болады.
Сондық тан, х – меншікті вектор, ал λ t – операторының меншікті мә ні болады.
1-салдар. Ә рбір ө зі тү йіндес толығ ымен ү зіліссіз оператордың ең болмаса бір меншікті мә ні болады.
Бұ л тұ жырым қ азір ғ ана дә лелденген теоремадан жә не 1-теореманың салдарынан шығ ады.
2-салдар. Ө зі тү йіндес толығ ымен ү зіліссіз t операторының ә рбір нө лден ерекше инвариант L кең істікасты оның меншікті векторын ұ стайды.
Дә лелдеме. t-мен бірге 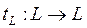 операторы да толығ ымен ү зіліссіз. Бұ л оператор 1-салдар бойынша меншікті λ j мә ніне ие болады, сондық тан, L-де
операторы да толығ ымен ү зіліссіз. Бұ л оператор 1-салдар бойынша меншікті λ j мә ніне ие болады, сондық тан, L-де  операторының, ал онда t операторының да меншікті векторы бар болады.
операторының, ал онда t операторының да меншікті векторы бар болады.
3-салдар. Ө зі тү йіндес толығ ымен ү зіліссіз оператордың мү лдем нү ктелік спектрі болады.
Дә лелдеме. Іс жү зінде, барлық меншікті векторларғ а инвариант С кең істікасты болады. Кері жағ дайда, ол 2-салдар бойынша меншікті векторды ұ стауғ а тиіс болар еді. Бұ л анық тамағ а қ айшы.
15-теорема. Ө зі тү йіндес толығ ымен ү зіліссіз t операторының меншікті мә ндерінің жиынының тең бір ғ ана  шектік нү ктесі болады.
шектік нү ктесі болады.
Дә лелдеме. Егер 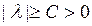 болатындай ә ртү рлі меншікті
болатындай ә ртү рлі меншікті 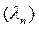 мә ндерінің ақ ырсыз тізбегі бар болса, онда сә йкес меншікті
мә ндерінің ақ ырсыз тізбегі бар болса, онда сә йкес меншікті 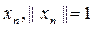 векторлары ү шін олардың ортонормальдылығ ынан
векторлары ү шін олардың ортонормальдылығ ынан  болғ анда
болғ анда  қ атынасы шығ ады. Бірақ бұ л жағ дайда
қ атынасы шығ ады. Бірақ бұ л жағ дайда 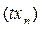 тізбегі компактылы болмас еді. Бұ л t операторының толық ү зіліссіздігіне қ айшы.
тізбегі компактылы болмас еді. Бұ л t операторының толық ү зіліссіздігіне қ айшы.