Лекция. Изоморфты сызықтық кеңістіктер.Базистен базиске өту кезінде вектор координаттарын түрлендіру.

Екі R, R^¢ сызық ты кең істіктерін изоморфты кең істіктер деп атайды, егер олардың элементтерінің арасында ө зара бір мә нді сә йкестік бар болып, ол сә йкестік келесі шарттарды қ анағ аттандырар болса: х элементіне х^¢ элементінің, у элементіне у^¢ элементінің сә йкес келуінен х + у элементіне х^¢ + у^¢ элементінің, a х элементіне a х^¢ элементінің сә йкес келуі шығ ады.

Екі сызық ты кең істік R, R^¢ изоморфты болса, онда R жиынының нө лдік элементіне R^¢ жиынының нө лдік элементі сә йкес келеді жә не керісінше.

Екі изоморфты кең істіктердің ө лшемдері бірдей болады. Ендеше, барлық n - ө лшемді кең істіктер R ⁿ координаттық кең істігіне изоморфты болады. Бұ л дегеніміз, басқ а n - ө лшемді кең істіктер R ⁿ координаттық кең істігінің «кө шірмесі» тә різді деген сө з.

1 - мысал. Бірінші параграфта келтірілген 2-мысалды алайық:

тү ріндегі реттелген нақ ты сандар жиыны. Бұ л жиын-ның элементтері базис болады.

Дә лелдейік. Бірінші тә сіл. Біріншіден кез келген 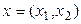элементі элементтері арқ ылы ө рнектеледі:

Сонымен қ атар, элементтерінің сызық ты тә уелсіздігі тек-серілуі керек. Ол ү шін олардың сызық ты комбинациясын нө лге тең естірейік:

,

,

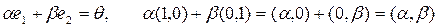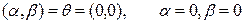яғ ни элементтері сызық ты тә уелсіз. Сонымен базистің екі шарты да орындалып тұ р: біріншіден, элементтері сызық ты тә уелсіз, екіншіден, осы элементтер арқ ылы сызық ты кең істіктің кез келген элементін ө рнектеуге болады.

Екінші тә сіл. Берілген элементтерінен екінші ретті анық тауыш қ ұ растырып есептейміз

= 1.

Анық тауыш нө лге тең емес, яғ ни берілген элементтер R ² кең істігінде базис болады.

Бұ л кең істікте базис жалғ ыз емес. элементтері де базис болады (тексерің із).

Белгілі бір элементтің ә ртү рлі базистердегі координаттарын есептеп кө рейік.

Осы кең істіктің 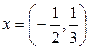элементін алайық. Бұ л элементтің базисіндегі жә не 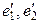базисіндегі координаталарын табайық.

; ;

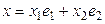. Бұ дан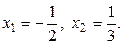

Сонымен,

.

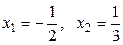сандары х элементінің базисіндегі координа-талары.

Енді екінші базисті қ арастырайық

;

; ; ;

.

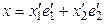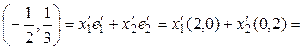
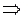
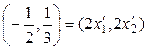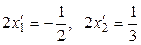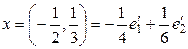сандары 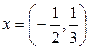элементінің базисіндегі координаталары.

Сонымен, 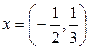элементінің ә ртү рлі базистегі координаталары ә рқ алай екенін кө рдік.

Іс жү зінде элементтердің сызық ты тә уелсіздігін тексеру ү шін олардың сызық ты комбинациясын нө лдік элементке q тең естіреміз. Осы тең діктен сызық ты комбинацияның барлық коэффициенттерінің 0 екендігі шығ ар болса элементтер сызық ты тә уелсіз. Ал коэффициенттердің кемінде біреуі нө л емес болса, элементтер сызық ты тә уелді болады.

2 - мысал. x = (-3, 1, 5), y = (6, -2, 15) элементтері сызық ты тә уелді ме?

Шешуі. Бұ лардың сызық ты комбинациясын нө лдік элементке q тең естіреміз

;

;

.

,

.

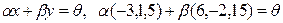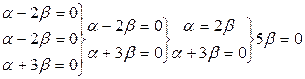Сонымен, сызық ты комбинацияның коэффициенттерінің бә рі 0 екен: . Ендеше бұ л векторлар сызық ты тә уелсіз болады.

3 - мысал. элементтері сызық ты тә уелсіз болып элементтері сызық ты тә уелді болса, онда у векторы элементтері арқ ылы ө рнектелетіндігін кө рсетің іздер.

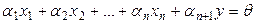Шешуі. векторлары сызық ты тә уелді болғ андық -тан, кемінде біреуі 0-ге тең емес сандары табылып тең дігі орындалады.

Мұ нда ө йткені болса, тең дігін алар едік те, 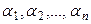сандарының кемінде біреуі 0-ге тең емес болады. Ал бұ л элементтерінің сызық ты тә уелсіз-дігіне қ айшы келеді.

Сонымен 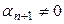. Онда 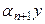мү шесін тең діктің екінші жағ ына шығ арамыз

Тең діктің екі жағ ында санына бө леміз де былай белгілейміз

.

Сонда у элементі элементтері арқ ылы сызық ты ө рнек-теледі екен.