Лекция. Евклид кеңістігі және олардың мысалдары. Банах кеңістігі және оның мысалдары. Сеперабельдік кеңістіктер

Екі вектордың скаляр кө бейтіндісi аналитикалық геометрия курсында анық талып, кейiн бұ л ұ ғ ым Rⁿ кең iстiгiнде жалпыланғ ан тү рде, дә л айтқ анда, кез-келген х = (х₁, х₂..., х_n) жә не у = (у₁, у₂..., у_n) векторлары ү шiн олардың скаляр кө бейтiндiсi (х, у) тү рiнде таң баланып, жә не

(х, у) = х₁у₁+, х₂у₂. +...х_n у_n

тең дігімен анық талғ аны белгілі.

Ендi скаляр кө бейтiндi ұ ғ ымын жалпы сызық тық кең iстiктерде анық тайық.

Е сызық тық кең істік берілген болсын.

1-а нық тама. Егер Е нің кез келген x, y элементтері ү шін анық талғ ан (x, y) - нақ ты мә нді функция

1)

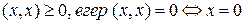
2)

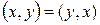
3)

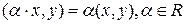
4)

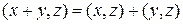
аксиомаларын қ анағ аттандырса, оны скаляр кө бейтінді деп атаймыз.

2-анық тама. Егер Е сызық тық кең істігінде скаляр кө бейтінді анық талғ ан болса оны Евклид кең істігі деп атайды.

Скаляр кө бейтіндінің 1)-4) аксиомаларын пайдаланып, оның мына тө мендегі қ асиеттерін кө рсетуге болады

;

;

;

;

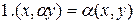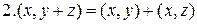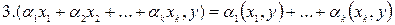Евклид кең істігінің кез келген элементінің скаляр (х, х) кө бейтіндісі оң сан. Сондық тан, бұ л (х, х) скаляр кө бейтіндіден квадрат тү бір - 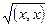алуғ а болады.

3-анық тама. Е - Евклид кең істігінің элементіне сә йкес келетін (х, х) скаляр кө бейтіндінің квадрат тү бірін - 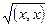оның нормасы деп атаймыз жә не оны ||x|| символымен белгілеп, мына 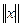= 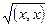формуламен ө рнектейміз.

1-тұ жырым. Кез келге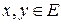н ү шін

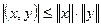
тең сіздігі орындалады.

Бұ л тең сіздікті Коши – Буняковский тең сіздігі дейді.

2-тұ жырым. 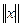= 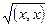ө рнегі норманың аксиомаларын қ анағ аттандырады.

Салдары. Кез келген Евклид кең істігі нормаланғ ан кең істік болады.