Сызықты кеңістіктің өлшемі мен базисі

Сызық ты кең істіктің 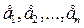элементтерінің сызық ты комбинациясы деп 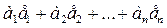- ө рнегін айтамыз, мұ ндағ ы 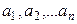- кез келген нақ ты сандар.

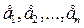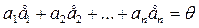Сызық ты кең істіктің элементтерін сызық ты тә уелді деп айтамыз, егер кемінде біреуі нө л емес сандары табы-лып тең дігі орындалар болса, ал осы тең діктен 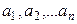сандарының бә рі де нө л екендігі шығ ар болса, яғ ни 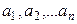онда 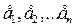элементтерін сызық ты тә уелсіз дейміз.

Сызық ты кең істіктің сызық ты тә уелсіз 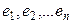элементтерін осы кең істіктің базисі деп атаймыз, егер ә рбір х элементі ү шін сандары табылып келесі тең дік орындалар болса,

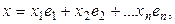
мұ ндағ ы 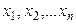сандарын х элементінің 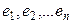базисіндегі координаталары деп атаймыз.

Сызық ты кең істікте n сызық ты тә уелсіз элементтер бар болып, ал кез келген n+1 элементтер сызық ты тә уелді болса, онда кең істік n -ө лшемді деп аталады.

Теорема 1. n-ө лшемді сызық ты кең істіктегі кез-келген n сызық ты тә уелсіз элементтер базис болады.

Басқ аша айтар болсақ, сызық ты кең істікте базис болатын элементтердің саны сызық ты кең істіктің ө лшеміне тең болады.Сызық ты кең істіктердің негізгі мысалдарын келтірейік.

1) Координаттық n - ө лшемді сызық ты кең істік. Кез келген рет – ретімен орналасқ ан n нақ ты сандардың 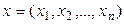тү ріндегі жиынын R ⁿ д еп белгілейік. Амалдарды былай анық таймыз: 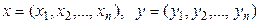элементтері ү шін қ осу амалы

;

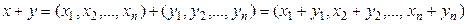элементті санғ а кө бейту амалы

Екі элементті қ осу ү шін олардың сә йкес координаттарын қ осады, ал элементті санғ а кө бейткенде, элементтің барлық координаттарын сол санғ а кө бейтеді.

Бұ л жиын сызық ты кең істік болады (тексерің із). R ⁿ кең істігі n - ө лшемді, ө йткені бұ л кең істікте

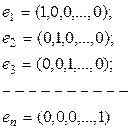
тү ріндегі n - элементтен тұ ратын сызық ты тә уелсіз элементтер жү йесі (яғ ни базис болатын) бар. Бұ л базисті кең істіктің стандартты базисі деп атайды. Ә рине, мү ндағ ы 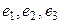элементтері де сызық ты тә уелсіз, бірақ бұ л ү ш элемент n -ө лшемді кең істікте базис бола алмайды, ө йткені олардың саны аздық етеді (n -ө лшемді кең істікте базис n элементтен тұ рады). Бұ л кең істікті кейде арифметикалық кең істік деп те атайды.

2) Матрицалар кең істігі. Ө лшемі m´ n болатын матрицалар жиынында кә дімгі матрицаларды қ осу жә не матрицаны санғ а кө бейту амалын қ арастыру арқ ылы сызық ты кең істік аламыз.

3) Кө пмү шеліктер кең істігі Р_n. Дә режесі берілген n санынан аспайтын, коэффициенттері нақ ты сан болып келетін кө пмү шеліктер жиыны. Кө пмү шеліктерге кә дімгі амалдарды қ олданамыз: кө пмү шеліктерді қ осу, кө пмү шелікті санғ а кө бейту. Кең істіктің стандартты базисі 1, t, t², t³, …, tⁿ. Базис n+1 элементтен тұ рады, яғ ни Р_n кең істігі n+1 - ө лшемді. Элементтері мынадай тү рде жазылады

P_n = a₀ tⁿ + a₁ t^n-1 + a₂ t^n-2 + … + a_n-1 t + a_n.

Егер n – ретті анық тауыш берілетін болса, онда оның ә рбір тік жолын немесе жә й жолын n - ө лшемді сызық ты кең істіктің элементі ретінде қ арастыруғ а болады. Мұ ндай жағ дайда кең істіктің элементтері ү шін мынадай белгілеулерді пайдалануғ а болады. Берілген

ï А ï =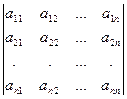

анық тауышының бірінші жә й жолының элементтерін х₁ элементінің координаттары ретінде қ арастырамыз х₁ = (а₁₁, а₁₂,..., а_1n).Анық тауыштың басқ а жә й жолдарының да элементтерін осығ ан ұ қ сас белгілейміз: х₂ = (а₂₁, а₂₂,..., а_2n),..., х_n = (а_n1, а_n2,..., а_nn).

Теорема 2. х₁ = (а₁₁, а₁₂,..., а_1n), х₂ = (а₂₁, а₂₂,..., а_2n),..., х_n = =(а_n1, а_n2,..., а_nn) элементтерінің сызық ты тә уелсіз болуы ү шін ï Аï ¹ 0 болуы қ ажетті жә не жеткілікті.

Жоғ арыда n-ө лшемді сызық ты кең істіктің кез-келген n сызық ты тә уелсіз элементтері базис болатыны айтылды. Ендеше n -ө лшемді сызық ты кең істіктің берілген n элементінің базис болатындығ ын тексеру ү шін, сол элементтерден анық тауыш қ ұ растырып есептеу керек. Анық тауыш нө лге тең емес болса, берілген элементтер базис болады. Анық тауыш нө лге тең болса берілген элементтер сызық ты тә уелді болғ аны, яғ ни базис болмайды.

Қ арастырылғ ан R ⁿ кең істігінің дербес жағ дайы R ² жә не R ³ кең істіктері.

R ² кең істігінің элементтері тү ріндегі реттелген сың арлы нақ ты сандар болып табылады. Бұ л кең істікте элементтері базис қ ұ райды.

R ³ кең істігінің элементтері 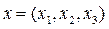тү ріндегі реттелген нақ ты сандар болып табылады. Бұ л кең істікте 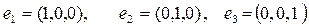элементтері базис болады, ал

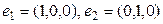элементтері базис бола алмайды, ө йткені ү ш ө лшемді кең істікте базис ү ш элементтен тұ рады.

Сызық ты кең істіктегі базис дегеніміз – жазық тық тағ ы немесе кең істіктегі тікбұ рышты координат жү йелерінің аналогы (ұ қ састығ ы) тә різдес. Жазық тық та XOY жә не X¢ O¢ Y¢ тікбұ рышты координат жү йелері берілсе, белгіленген бір нү ктенің екі тү рлі координаталары бар: біреуі XOY жү йесінде де, екіншісі X'O'Y' жү йе-сінде.

Сонымен қ атар, бұ л координаталардың бір-бірімен байланысын да біз аналитикалық геометриядан білеміз: 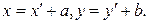Осы айтылғ андарғ а ұ қ сас, сызық ты кең істіктің элементінің ә ртү рлі базистегі координаталары да ә ртү рлі болады.