Лекция. Оператордың графигі және тұйықталған операторлар. Хан-Банах теоремасы және оның салдары

Ө зі тү йіндес операторды жә не тұ йық тама операциясын ә рі қ арай зерттеу мақ сатымен оператордың графигі ұ ғ ымын енгіземіз.

Гильберт кең істігі -тың екі данасын қ арайық жә не 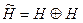осы кең істіктердің тура қ осындысы болсын делік, яғ ни сызық тық операциялардың кә дімгі анық тамларымен анық талғ ан қ осақ тар жиынтығ ы. Ә рі қ арай 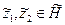ү шін осы элементтердің скаляр кө бейтіндісін тең дігі кө мегімен анық таймыз. Скаляр кө бейтіндінің барлық қ асиеттері орындалатын тексеру қ иын емес. Гильберт кең істігінің қ алғ ан аксиомалары да тү гел орындалады. Сондық тан, 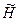-та гильберт кең істігі болады.

Егер H кең істігінде сызық тық A операторы берілсе, онда тү ріндегі элементтердің 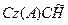жақ ын, бұ рынғ ыша, A операторының графигі деп атаймыз. A операторымен бірмә нді анық талатын сызық тық кө пбейне екенін оң ай кө руге болады. Керісінше егер A жә не B екі операторы ү шін 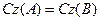болса, онда A=B болады. Ең соң ында A операторы тұ йық болуы ү шін H кең істігінің тұ йық кең істікасты болуы қ ажетті жә не жеткілікті екенін тексеру қ иын емес. 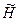-та 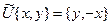тең дігімен анық талатын 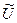операторын қ арайық.

жә не 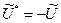екeні тү сінікті, содан 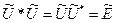яғ ни 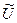-унитар оператор

1-Лемма. Егер A бар жерде тығ ыз сызық тық D(A) кө пбейнесінде анық талғ ан кез-келген сызық тық оператор болса, онда 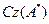сызық тық 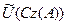кө пбейнесіне ортогонал толық тауыш болады.

Дә лелдеме. 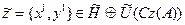босын делік. Бұ л < (), { }> =0 екенін білдіреді. Бұ дан жә не, сондық тан, жә не яғ ни .

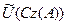Пайымдауларды кері тә ртіпте қ айталап, -тен осы элементтің -дағ ы кез-келген элементке ортогонал екенін аламыз жә не лемме дә лелденді.

3-теoрема, Егер A H -та бар жерде тығ ыз D(A) жиынында анық талғ ан тұ йық оператор болса онда 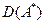-да бар жерде тығ ыз жә не 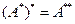бірмә нді анық талғ ан. Ә рі .

Дә лелдеме. A тұ йық болатындық тан Cz(A) тұ йық сызық тық кө пбейне болады жә не, демек, 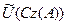-да тұ йық. Сондық тан

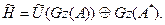/3/

Тең діктің екі бө лігіне де унитар 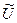операторын қ олданып, жә не, біріншіден, 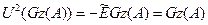жә не, екіншіден, унитар операторортогонал элементтерді ортогонал элементтерге кө шітінін ескере отырып

/4/

екенін аламыз.

Алдымен, 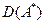бар жерде тығ ыз екенін кө рсетейік. Егер бұ лай болмаса, онда 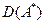-ғ а ортогонал мү лдем ерекше, 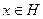бар болады. элементі 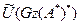-ғ а ортогонал болады, себебі кез-келген ү шін

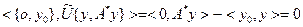
Сондақ тан, 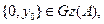бұ дан 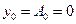. Алынғ ан қ айшылық біздің ұ йғ арымымызды дә лелдейді.

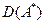бар жерде тығ ыз болғ андық тан A^** бірмә нді анық талады. A^** =A тең дігін дә лелдеу ү шін /4/ қ атынасты жә не лемманы пайдалану жеткілікті.

4-теорема. A^** операторы сонда, тек сонда ғ ана бар болады, егер бар жерде тығ ыз жиында анық талғ ан A операторының тұ йық тамасы болса. Бұ л жағ дайда A^** =A.

Дә лелдеме. Егер A -ның 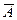тұ йық тамасы болса, онда 3-теорема бойынша бар болады жә не Бірақ 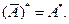, сондық тан, , бұ дан A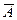^** = жә не теореманың I-бө лігі дә лелденді.

A^** бар болсын делік. /3/-ті A^* -ғ а қ олданып, біз

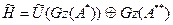/5/

екенін аламыз. Басқ а жағ ынан, 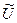операторын 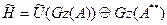тең дігінің екі бө лігіне қ олдана отырып

екенін аламыз. /5/ пен /6/-ны салыстырудан екені шығ ады, яғ ни А -ның тұ йық кең ейтілуі 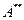болады.

Шектеусіз операторлар ү шін тағ ы инвариант кең істікасты ұ ғ ымын енгізуге болады.

Егер

І/ дан шық са,

ІІ/ барлық 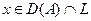ү шін 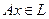шық са/ яғ ни барлық ү шін 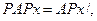, онда L кең істікасты A операторының инвариант кең істікасты деп аталады.

1/-ден жә не D(A) -ның H- та тығ ыздығ ынан 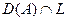-де бар жерде тығ ыздығ ы шығ ады.

Шектеусіз симметриялы операторлар ү шін L -дің инварианттылығ ынан 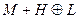-дің инварианттылығ ы шығ атынын кө рсетейік. Іс жү зінде, жә не 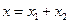болсын делік, мұ нда 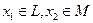L - инвариант кең істікасты болғ андық тан жә не D(A) -сызық тық кө пбейне болғ андық тан болады.

Ә рі қ арай, егер 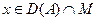жә не y 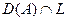-деп кез-келген элемент болса, онда себебі 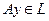жә не 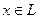. Сонымен Ax элементі 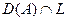-ге ортогонал, ал бұ л кө пбейне L -де бар жерде тығ ыз болғ андық тан 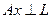, бұ дан .

Егер L A операторының инвариант кең істікасты болса, онда біз бұ рынғ ыша L A -ны жетектейді /приводит/ дейміз.

5-теорема. L кең істікасты симметриялық A операторын сонда, тек сонда ғ ана жетектейді, егер осы кең істікасты ү стіне проекциялайтын P операторы A -мен ауыстырымды болса.

Дә лелдеме. L -нвариант кең істікасты болсын делік. Сонда, егер болса, онда 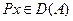жә не 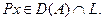L -дің инварианттылығ ының 2/ шартынан

/7/

/7/ мен /8/ -ден екені шығ ады жә не A -ның шектеулі P операторымен ауыстырымдылығ ы дә лелденді.

Керісінше, A мен P ауыстырымды болсын делік. Онда, ең алдымен -дан 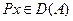шығ ады.

Ә рі қ арай, 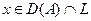ү шін 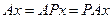, яғ ни 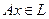жә не L -дің инварианттылығ ы дә лелденді.