Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция. Гильберт кеңістігі және оның мысалдары. Гильберт кеңістігінде Фурье қатары
|
|
1 -анық тама. Н – Евклид кең істігі берілген болсын.Егер Н толық, ақ ырсыз ө лшемді болса, оны Гильберт кең істігі дейді.
Айталық, Н Гильберт кең істігінде { ek }- ортонормал жү йе берілген болсын,
2 -анық тама. 
- сандарын хÎ Н элементінің Фурье коэффициенттері, ал 
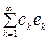қ атарын Фурье қ атары дейді.
Фурье қ атарының жинақ тылық қ а зерттейік. Ол ү шін қ андайда бір ak тұ рақ тыларын алып,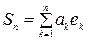 
қ осындыны зерттейік:
Демек,
Егер бұ л тең дікте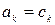 
болса, онда
болады. Бұ дан 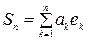тү ріндегі қ осындыларының ішінде х элементке ең жақ ын тұ ратыны Фурье қ атарының n – дербес қ осындысы болатыны кө рініп тұ р.
Егер 
екенін есепке алсақ, бұ дан
тең сіздігі келіп шығ ады. Бұ л тең сіздікте 
шекке ө тсек, онда
тең сіздігіне ие боламыз. Бұ л тең сіздікті Бессель тең сіздігі дейді.
Егер
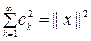
тең дігі орынды болса, оны Парсеваль тең дігі дейді.
3 -анық тама. Егер{ ek } жү йеде Н - Гильберт кең істігінің кез келген х элементі ү шін Парсеваль тең дігі орындалса бұ л жү йені тұ йық жү йе дейді.
Егер{ ek } жү йе тұ йық болса, онда
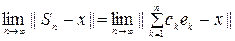
болады, яғ ни х тің Фурье қ атары сол элементке жинақ талады.
1-теорема (Рисс-Фишер). Н -Гильберт кең істігінде { ek } ортонормал жү йе жә не 
шартты қ анағ аттандыратын сk – сандар тізбегі берілген болсын.
Онда Н кең істігіне тиісті х элементі табылып: сk -лар х элементінің Фурье коэффициенттері, яғ ни жә не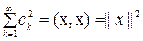 
болады.
Енді Гильберт кең істігінің кейбір ішкі кең істіктерін қ арастырамыз.
Гильберт кең істігі нормаланғ ан кең істік болғ андық тан, оның ішкі кең істіктерін нормаланғ ан кең істіктердегі сияқ ты анық таймыз.
Демек, Н тің ішкі кең істігі - тұ йық болғ ан сызық тық кең істіктер.
1 -мысал. Н гильберт кең істігінен кез келген z элементін аламыз. Егер
М ={x: xÎ Н, x^z }, яғ ни Н тің z элементке ортогонал болғ ан барлық нү ктелері жиыны болса, онда М жиыны Н тің ішкі кең істігі болады.
Шешуі. Алдымен М сызық ты жиын болатынын кө рсетейік. x, yÎ М, " l Î R болсын. Онда
(x+y, z)= (x, z)+(y, z)=0 Þ x+yÎ М;
(l x, z)= l (x, z)=0 Þ l xÎ М;
Енді М нің тұ йық болатынын дә лелдейміз. М тұ йық Û " xn Î М жә не xn ® а Þ а Î М, яғ ни М ді тұ йық дейміз, егер де М жиынына тиісті " xn тізбегінің шегі а сол жиынғ а тиісті болса.
Айталық, xn Î М жә не xn ® а болсын.
Онда, || xn - а||2=(xn - а, xn - а)® 0, n® ¥,
Þ |(xn - а, xn - а)|= || xn||2-2(а, xn) +||a||2 Þ |(а, xn)|£ || xn||2-||a||2.