
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функцияны интерполяциялау мәселесі.
|
|
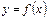 функциясы берiлген жә не оның мә ндерi
функциясы берiлген жә не оның мә ндерi 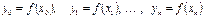 кесте тү рiнде берiлген.
кесте тү рiнде берiлген. 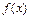 – функциясы сияқ ты
– функциясы сияқ ты 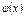 – кез келген функциясы да
– кез келген функциясы да 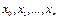 нү ктелерiнде дә л сондай мә ндердi қ абылдайды, ал берiлген аралық тағ ы ө зге нү ктелерде
нү ктелерiнде дә л сондай мә ндердi қ абылдайды, ал берiлген аралық тағ ы ө зге нү ктелерде 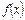 функциясының қ абылдайтын мә нiне, таң далынғ ан дә лдiкпен алғ андағ ы, маң айлас шамағ а тең.
функциясының қ абылдайтын мә нiне, таң далынғ ан дә лдiкпен алғ андағ ы, маң айлас шамағ а тең.
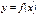 функциясын берiлген тораптардан ө зге нү ктелерде
функциясын берiлген тораптардан ө зге нү ктелерде 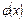 функциясымен алмастырса, мұ ндай операцияны
функциясымен алмастырса, мұ ндай операцияны 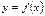 функциясын интерполяциялау деймiз. Мұ нда
функциясын интерполяциялау деймiз. Мұ нда 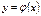 формуласы интерполяциялау формуласы деп аталады. Интерполяциялау формулалары
формуласы интерполяциялау формуласы деп аталады. Интерполяциялау формулалары 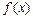 функциясының аргументтiң берiлген мә ндерi қ арастырылғ ан аралық та белгiсiз мә ндерiн табу ү шiн қ олданылады.
функциясының аргументтiң берiлген мә ндерi қ арастырылғ ан аралық та белгiсiз мә ндерiн табу ү шiн қ олданылады.
Нә тижесiн шығ арар кезде мынадай қ ателiктер ескерiледi:
1. Ә дiс қ ателiгi
2. Жойып алмау қ ателiгi
3. Жуық тау қ ателiгi.
Ә дiстiң қ ателiгi қ алғ ан мү шенi
интерполяциялау формуласы арқ ылы табылуы мү мкiн жә не  – тiң сә йкес дә режесiндегi туындысының интерполяциялау аралығ ындағ ы мә нiне байланысты бағ аланады.
– тiң сә йкес дә режесiндегi туындысының интерполяциялау аралығ ындағ ы мә нiне байланысты бағ аланады.
9.2. Тең емес арақ ашық тық та орналасқ ан тү йiндерге арналғ ан Лагранждың интерполяциялық формуласы
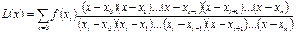 (1)
(1)
Айталық, 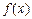 функциясы
функциясы 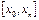 аралығ ында тек
аралығ ында тек 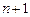 -ге дейiнгi барлық дә режеде туындысы табылады жә не қ ателiгi мына тү рде болады.
-ге дейiнгi барлық дә режеде туындысы табылады жә не қ ателiгi мына тү рде болады.
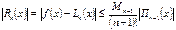 (2)
(2)
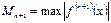 ,
,
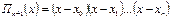
9.3. Тең емес арақ ашық тық та орналасқ ан тү йiндерге арналғ ан Ньютонның интерполяциялық формуласы
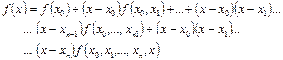 (3)
(3)
(3)-тiң оң жағ ындағ ы барлық мү шелерiнiң қ осындысы Ньютонның интерполяциялау кө пмү шелiгi деп, ал соң ғ ы мү шесi
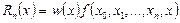 (4)
(4)
қ ателiгi деп аталады.
9.4. Эйткеннің интерполяциялау сұ лбасы
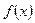 Функциясын есептегенде
Функциясын есептегенде 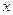 -тiң нақ ты мә ндерiн тең емес арақ ашық тық та орналасқ ан аргументтерi ү шiн Лагранждың интерполяциялау полиномы арқ ылы Эйткеннiң сұ лбасын қ олдану тиiмдi.
-тiң нақ ты мә ндерiн тең емес арақ ашық тық та орналасқ ан аргументтерi ү шiн Лагранждың интерполяциялау полиномы арқ ылы Эйткеннiң сұ лбасын қ олдану тиiмдi.
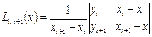
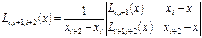 (5)
(5)
…………………………………….

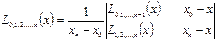
болсын жә не Эйткен сұ лбасы бойынша есептеу тө мендегi сұ лба тү рiнде жү ргiзiледi:
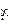
| 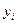
| 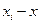
| 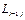
| 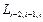
| 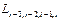
| |
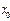
| 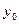
| 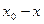
| ||||
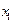
| 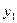
| 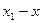
| 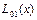
| |||
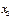
| 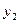
| 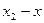
| 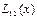
| 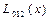
| ||
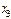
| 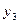
| 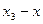
| 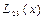
| 
| 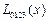
| |

| 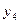
| 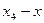
| 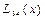
| 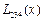
| 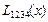
| 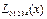
|
Есептеу соң ғ ы 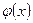 -тiң тiзбектiк мә нiн салыстырумен анық талады.
-тiң тiзбектiк мә нiн салыстырумен анық талады.
9.5. Ньютонның бірінші интерполяциялау формуласы
Тұ рақ ты қ адаммен берілген кесте, функцияғ а ақ ырлы тү рлі кестесі қ ұ рылғ ан. Интерполяциалау кө п мү шелігін осындай тү рде іздейміз:
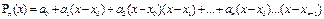 (6)
(6)
Бұ л n дә режедегі кө пмү шелік.
 коэфиценттерінің мағ ынасын, шық қ ан функцияның мағ ынасының сә йкестік шартын жә не кө пмү шелік тү йіндерін табамыз.
коэфиценттерінің мағ ынасын, шық қ ан функцияның мағ ынасының сә йкестік шартын жә не кө пмү шелік тү йіндерін табамыз. 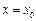 -ге қ арап, (5.11)-ден
-ге қ арап, (5.11)-ден 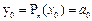 -ді табамыз, одан
-ді табамыз, одан 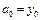 .
. 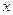 мә нді
мә нді 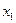 жә не
жә не 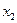 -ні бере отырып тө мендегіні аламыз:
-ні бере отырып тө мендегіні аламыз:
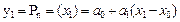 , одан
, одан 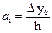
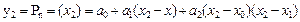
тағ ы сол сияқ ты 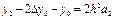 , немесе
, немесе 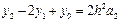
одан 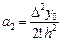
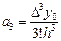 .
.
Жалпы жағ дайда 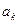 ү шін мынадай тү р болады:
ү шін мынадай тү р болады:
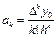 (7)
(7)
(6)-ші кө пмү шелік ү шін (7)-ні қ оямыз:
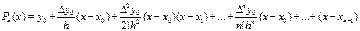 (8)
(8)
Бұ л формула басқ аша тү рде қ олданылады
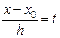 болса, тағ ы сол сияқ ты
болса, тағ ы сол сияқ ты 
онда: 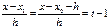
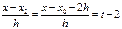
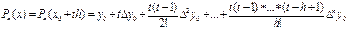 (9)
(9)
(9) – формула Ньютонның бірінші интерполяциондық формуласы деп аталады. Абсолюттік шамасы бойынша  кіші болғ анда, бұ л формула интерполяцианың кесіндісінің басында интерполяциалау ү шін қ олданылады. Осы себепке байланысты Ньютонның бірінші интерполяциалау формуласын алғ а интерполяциалау деп атайды. Бастапқ ы
кіші болғ анда, бұ л формула интерполяцианың кесіндісінің басында интерполяциалау ү шін қ олданылады. Осы себепке байланысты Ньютонның бірінші интерполяциалау формуласын алғ а интерполяциалау деп атайды. Бастапқ ы 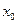 мә нін
мә нін 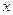 аргументтегі кестелік мә нді қ абылдауғ а болады.
аргументтегі кестелік мә нді қ абылдауғ а болады.
9.6. Ньютонның екінші интерполяциялау формуласы
Аргументтің мә ні интерполяциалау кесіндісінің соң ына жақ ын орналасқ ан кезде бірінші интерполяциалау формуласын қ олдану тиімсіз. Бұ л жағ дайда артқ а интерполяциалау, яғ ни, Ньютонның келесі тү рде ізделінетін екінші интерполяциалау формуласы қ олданылады:
 (10)
(10)
Ньютонның бірінші формуласындағ ыдай 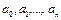 коэффицентері тү йінде функция мә ндері жә не интерполяциалау кө пмү шесінің сә йкес келу шартынан табылады.
коэффицентері тү йінде функция мә ндері жә не интерполяциалау кө пмү шесінің сә йкес келу шартынан табылады.
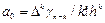 (11)
(11)
(11)-шы ө рнекті (10)-ші ө рнекке қ ойып жә не 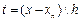 айнымалысына ө тіп, Ньютонның екінші формулаларының соң ғ ы тү рін аламыз:
айнымалысына ө тіп, Ньютонның екінші формулаларының соң ғ ы тү рін аламыз:
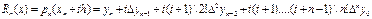 (12)
(12)
9.7. Интерполяциалау кө пмү шелігінің қ ателігі
Егер 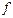 интерполяциалау функциясы аналитикалық тү рде белгілі болса, онда интерполяциалау қ ателігін (ә діс қ ателігі) бағ алауғ а арналғ ан формуланы қ олдануғ а болады.
интерполяциалау функциясы аналитикалық тү рде белгілі болса, онда интерполяциалау қ ателігін (ә діс қ ателігі) бағ алауғ а арналғ ан формуланы қ олдануғ а болады. 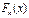 интерполяциалау кө пмү шелігінің қ алдық мү шесі мынадай болады:
интерполяциалау кө пмү шелігінің қ алдық мү шесі мынадай болады:
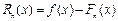
Бекітілген кесіндісі ү шін интерполяциалау кө пмү шелігінің бір ғ ана екендігінен, қ ателігі туралы сұ рақ ты баяндау Лагранж кө пмү шелігі мен Ньютон кө пмү шелігіне бірдей.
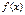 функциясының
функциясының 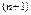 -ге дейінгі барлық туындыларды бар болсын деп ұ йғ арайық, R-тұ рақ ты кө бейткіш деп қ осымша функция енгіземіз:
-ге дейінгі барлық туындыларды бар болсын деп ұ йғ арайық, R-тұ рақ ты кө бейткіш деп қ осымша функция енгіземіз:
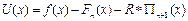 (13)
(13)
Байқ ап отырғ анымыздай, 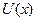 функциясының (
функциясының ( ) тү бірлері (
) тү бірлері (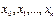 -интерполяциалау тораптары) бар. R-коэффициентін
-интерполяциалау тораптары) бар. R-коэффициентін 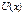 ә рбір
ә рбір 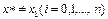 нү ктесінде (
нү ктесінде (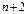 )-ші тү бір болатындай етіп таң дап аламыз. Шынында
)-ші тү бір болатындай етіп таң дап аламыз. Шынында 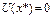 , яғ ни
, яғ ни
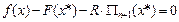 болуы ү шін
болуы ү шін
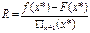 (14)
(14)
болуы жеткілікті. Сонымен, 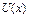 функциясының R мағ ынасы интерполяциалаудың кесіндісінде
функциясының R мағ ынасы интерполяциалаудың кесіндісінде 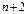 тү бірін иемденді жә не
тү бірін иемденді жә не 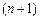 кесінділерінің ә рқ айсысының соң ында 0-ге айналды:
кесінділерінің ә рқ айсысының соң ында 0-ге айналды:
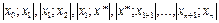
Кесінділердің ә рқ асыларына Рош теоремасын қ олдана отырып, мынағ ан кө з жеткіземіз:
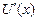 кем дегенде
кем дегенде 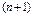 тү біріне ие.
тү біріне ие.
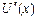 кем дегенде
кем дегенде 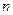 тү біріне ие.
тү біріне ие.
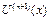 кем дегенде бір тү бірді иемденеді.
кем дегенде бір тү бірді иемденеді.
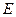 -ні
-ні 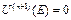 болатын нү ктенің ө зі деп белгілейік (13),
болатын нү ктенің ө зі деп белгілейік (13), 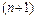 -рет дифференциялаймыз.
-рет дифференциялаймыз.
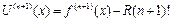
бұ дан 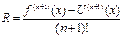
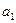
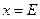 кезінде
кезінде
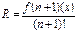 (15)
(15)
(14) пен (15)-ті салыстырсақ
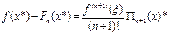
Бірақ 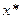 нү ктесі туынды (шынында
нү ктесі туынды (шынында 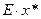 -қ а бағ ынышты!). Сондық тан былай жазуғ а болады.
-қ а бағ ынышты!). Сондық тан былай жазуғ а болады.
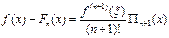
Егер 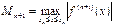 -ті қ абылдасақ, онда
-ті қ абылдасақ, онда
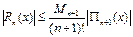 (16)
(16)
Бағ алау формуласын (5.21) Лагранж формуласы бойынша интерполяциялаудың ә діс қ ателігін есептеуге тікелей қ олданса болады. 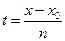 жә не
жә не 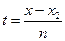 алмастыруды қ олдана отырып (16) формуласынан Ньютон формулалары бойынша интерполяциалаудың қ ателіктерін бағ алау формуласын алуғ а болады.
алмастыруды қ олдана отырып (16) формуласынан Ньютон формулалары бойынша интерполяциалаудың қ ателіктерін бағ алау формуласын алуғ а болады.
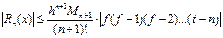 (17)
(17)
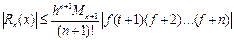 (18)
(18)
Лагранж жә не Ньютонның интерполяцияланғ ан кө пмү шелерінің талдауы, сондайақ (16), (18) бағ алау формулаларының талдаулары. Пайдалы практикалық қ ортындыларын жасауғ а мү мкіндік береді.
Қ ателік мә н мағ ынасына 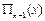 шамасы шешімді ә сер етеді, ол тү йінді нү ктелерді интервалының ортасынан
шамасы шешімді ә сер етеді, ол тү йінді нү ктелерді интервалының ортасынан 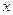 алынғ ан жағ дайда азайтылады. Сонымен қ атар,
алынғ ан жағ дайда азайтылады. Сонымен қ атар, 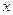 екі тү йінді мағ ыналардың ортасына жақ ын болғ анда
екі тү йінді мағ ыналардың ортасына жақ ын болғ анда 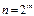 тү йіндерінің жұ п сандарын алғ ан тиімді (
тү йіндерінің жұ п сандарын алғ ан тиімді (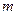 тү йіндерінен сол жақ тан жә не
тү йіндерінен сол жақ тан жә не 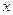 -тен оң жақ тан)
-тен оң жақ тан)
Егер 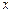 тү йінді мағ ыналардың біріне жақ ын болса,
тү йінді мағ ыналардың біріне жақ ын болса, 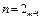 тү йіндердің тақ санын пайдалануғ а болады.
тү йіндердің тақ санын пайдалануғ а болады.
Ньютонның интерполяцияланғ ан формулаларын тә жірибеде қ ұ растыру кезінде сә йкес соң ғ ы қ алдық тары нө лге тең немесе жақ ын мү шелерді елемеу керек. Сондық тан, тә жірибелік есептеулерде Ньютонның интерполяцияланғ ан формулалары берілген дә лдік шегінде тұ рақ ты деп саналатын қ алдық тарғ а ие мү шелерге бө лінеді.
Соң ғ ы қ алдық тармен Ньютон формулалары бойынша интерполяциалау дә лдігі арасындағ ы байланыс келесі тү сініктемелермен бекітіледі.
Назар аударамыз: 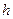 аз мә нінде жә не
аз мә нінде жә не 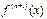 ү здіксіз жағ дайда, шамамен есептеуге болады:
ү здіксіз жағ дайда, шамамен есептеуге болады:
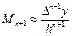
мұ нда 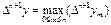
яғ ни, 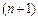 ретіндегі соң ғ ы қ алдық тар модульдерінен максималды. Сонымен (17) жә не (18).
ретіндегі соң ғ ы қ алдық тар модульдерінен максималды. Сонымен (17) жә не (18).
Ньютонның бірінші жә не екінші интерполяциялау формулаларының қ алдық мү шелерін бағ алау жағ дайлары мынадай тү рге ие:
 (19)
(19)
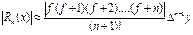 (20)
(20)
(19) жә не (20) формулалары 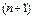 туынды интерполяциялаушы
туынды интерполяциялаушы 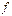 функциясын зерттемей ақ интерполяциалау ә дісінің қ ателігін бағ алауғ а мү мкіншілік беретіндігімен ың ғ айлы (соның ішінде,
функциясын зерттемей ақ интерполяциалау ә дісінің қ ателігін бағ алауғ а мү мкіншілік беретіндігімен ың ғ айлы (соның ішінде, 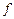 аналитикалық формуласы тіптен белгісіз болғ анда).
аналитикалық формуласы тіптен белгісіз болғ анда).
Интерполяциалау соң ғ ы қ ателігіне есептеу қ ателігі де ә сер етеді. Бұ л мә селелерді толық зерттеу аз қ иындық тар тудырмайды мысалы сенімді жә не кө п мә нді есептеу кестелерін қ ұ растыру кезінде.
Разрядтардың ү лкен санымен жә не кестелердің автоматтандырылғ ан басылымдарымен есеп жү ргізуге мү мкіндік беретін ЭЕМ-гі қ олданумен техникалық жұ мыс бірталай жең ілдейді.
9.8. Функция кестесін тығ ыздау
Функцияның кестесін тығ ыздау ү шін интерполяциалау қ олданылады. Функцияның берілген кестесі бойынша аргументтің мә нін ү лкейту арқ ылы жаң а кестені қ ұ ру операциясы кейбір жағ дайда функцияны субтабуляциялау деп аталады. Егер кесте тұ рақ ты қ адаммен берілген болса, онда Ньютонның интерполяциалау кө пмү шелігін қ олданғ ан жө н. ЭЕМ-де есептеу ү шін тү йіндік нү ктелері белгілі болғ ан жағ дайда (егер ақ ырлы айырымдар жә не полином дә режесі қ олмен есептелінген болса) Ньютон формулаларын Горнер кестесі арқ ылы кө рсетуге ың ғ айлы болады. Ньютонның бірінші интерполяциалау формуласы келесі тү рде кө рсетіледі:

Егер Горнер кестесін қ олдансақ 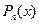 мә нін циклда есептеуімізге болады. Егер қ олданылатын ақ ырлы айырмдардың максималды реті ү лкен болмаса, онда
мә нін циклда есептеуімізге болады. Егер қ олданылатын ақ ырлы айырмдардың максималды реті ү лкен болмаса, онда 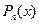 мә нін Ньютон формулалары арқ ылы табуғ а болады.
мә нін Ньютон формулалары арқ ылы табуғ а болады.
МЫСАЛ 1.
Мына мә ндер кестесi ү шiн Лагранж кө пмү шелiгiн қ ұ рып 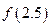 -тi есептең iз:
-тi есептең iз:
| x | ||||
| y |
Шешуi. тө мендегi жағ дайда n=3, онда 
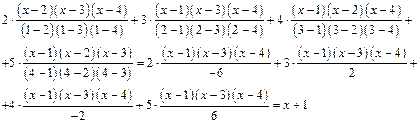
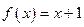 сызық тық функциясы интерполяциялациялау кө пмү шелiгi болып табылады, онда
сызық тық функциясы интерполяциялациялау кө пмү шелiгi болып табылады, онда
Жауабы: 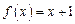
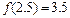 .
.
МЫСАЛ 2.
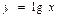 функциясының мә ндер кестесi берiлген.
функциясының мә ндер кестесi берiлген.
| x | ||||||
| y | 3.0000000 | 3.0043214 | 3.00806002 | 3.0128372 | 3.0170333 | 3.0211893 |
n=3 жоғ арғ ы Ньютонның бiрiншi формуласын қ олданып, lg1001 есептеп жә не R3 -қ алдық мү шесiн бағ алап кө рсетiң iз.
Шешуi.
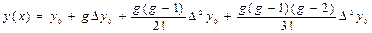
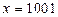 ү шiн,
ү шiн, 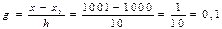
| x | y | 
| 
| 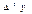
|
| 3.0000000 | 0.0043214 | -0.0000426 | 0.0000008 | |
| 3.0043214 | 0.0042788 | -0.0000418 | 0.0000009 | |
| 3.00806002 | 0.0042370 | -0.0000409 | 0.0000008 | |
| 3.0128372 | 0.0041961 | -0.0000401 | ||
| 3.0170333 | 0.0041560 | |||
| 3.0211893 |
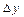 -тi есептеймiз:
-тi есептеймiз:
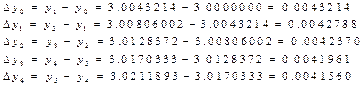
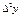 -тi есептеймiз:
-тi есептеймiз:
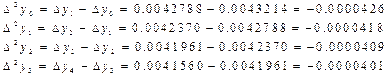
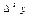 -тi есептеймiз:
-тi есептеймiз:
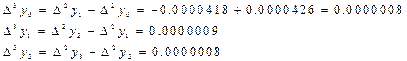
Осыдан,
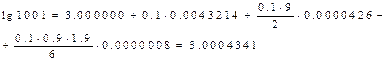
қ алдық мү шенi бағ алаймыз
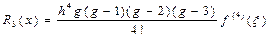 ,
,
мұ ндағ ы 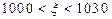 Егер
Егер 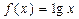 , онда
, онда 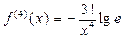 , сондық тан
, сондық тан 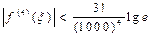
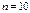 жә не
жә не 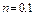 болса
болса
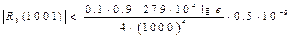
болады.
Жауабы: 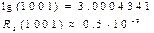
Бақ ылау сұ рақ тары:
1. Кестемен берілген функцияны интерполяциалау ә дісімен жуық таудың ерекшелігі неде?
2. Интерполяциалау кө пмү шелігінің табылуы мен жалғ ыздығ ы қ алай негізделеді? Оның дә режесі интерполяциалау тү йіндерімен қ алай байланысады?
3. Лагранж жә не Ньютонның интерполяциалау кө пмү шеліктері қ алай қ ұ рылады? Бұ л интерполяциалаудың екі ә дісінің ерекшкліктері қ андай?
Дә ріс. Сандық интегралдау. Интегралдық тегістеу. Интерполяциялық квадратуралық формулалары. Ең жақ сы алгебралық дә лдікті квадратуралық формулалар.