Рунге-кутт әдісі

Коши есебін қ арастырайық. 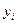арқ ылы ізделінді шешімнін 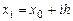нү ктесіндегі жуык мә нін белгілейік. Рунге-Кутт ә дісі бойынша ізделінді функцяның мә ндер тізбегін есептеу формуласы

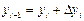
мұ ндағ ы

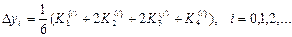
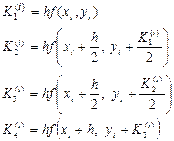
Бағ алау қ ателігі

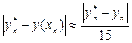
мұ ндағ ы 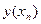– 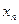нү ктесіндегі берілген тең деудін шешімінін дә л мә ні,

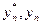- мә ндері h/2 жә не h қ адаммен алынғ ан жуық мә ндер.

МЫСАЛ 1.

Коши есебінің [0; 0, 2] кесіндіде e=10^-5 дә лдігімен жуық шешімін табу керек

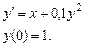
Шешуі. Бастапқ ы жуық тауды келесі тү рде аламыз

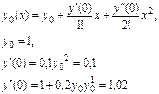
осыдан 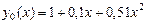. (3)-ші формуланы қ олдансақ

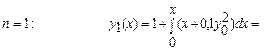
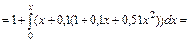(4)

.

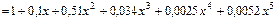Келесі айырым x =0, 2 болғ анда e мә нінен ү лкен болады

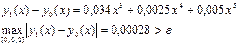
(4) ө рнектегі соң ғ ы екі қ осындылардын косындысы e шамасынан кіші, сондық тан 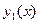келесі тү рде алуғ а болады

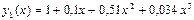
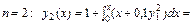
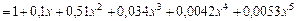
Келесі айырым [0; 0, 2] кесіндісінде e мә нінен кіші

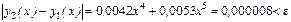
Жауабы: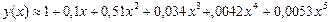

МЫСАЛ 2.

Коши есебімен

анық талғ ан, қ адамы 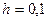болғ анда у функциясының тө рт мә нін Эйлер ә дісін қ олдана отырып табу керек.

Шешуі. Бастапқ ы шарттан 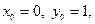сондық тан аргумент мә ндері

у функциясының мә ндері

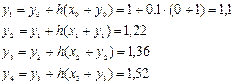
Жауабы:

МЫСАЛ 3.

Бірінші ретті дифференциалдық тең деудің шешімін Рунге-Кутт ә дісімен табу керек

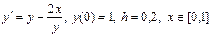
Шешуі.

Есептің шарты бойынша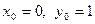

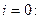
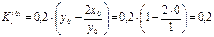
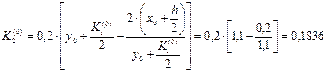
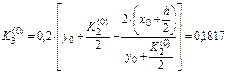
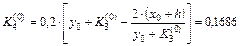
Осыдан

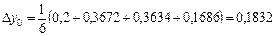
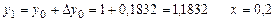болғ анда

.

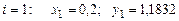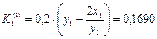
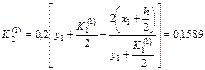
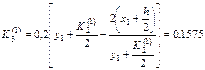
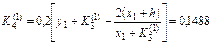
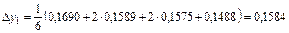
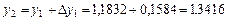
Осы сияқ ты мә ндеріне сә йкес 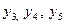функция мә ндерін табамыз.

13, 14, 15-Дә рістер. Математикалық физика есептерін шешудің сандық ә дістері. Дербес туындылы тең деудiң сандық шешiмi Пуассон тең деуіне қ ойылғ ан айырымдылық Дирихле есебінің жинақ тылығ ы мен орнық тылығ ы.

13.1. Торлар ә дісі