
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дирихле есебі үшін торлар әдісі.
|
|
Бiрiншi шектiк есеп немесе Пуассон тең деуi ү шiн
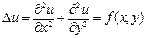 (2)
(2)
Дирихле есебi: Қ андай да бiр G облысының iшiнде (2) тең деудi қ анағ аттандыратын, ал Г шекарасында
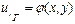 (3)
(3)
шартын қ анағ аттандыратын 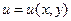 формуласын табу керек, мұ ндағ ы
формуласын табу керек, мұ ндағ ы 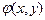 – берiлген ү зiлiссiз функция.
– берiлген ү зiлiссiз функция.
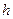 жә не
жә не 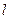 қ адамдарын сә йкес х жә не у деп таң дап, тор тұ рғ ызамыз
қ адамдарын сә йкес х жә не у деп таң дап, тор тұ рғ ызамыз 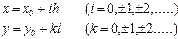 жә не ә рбiр iшкi
жә не ә рбiр iшкi 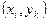 тү йiнiнде
тү йiнiнде 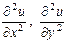 туындыларын (1) ақ ырлы айырымдар қ атынасымен алмастырып (2) тең деудi мына тү рде жазамыз:
туындыларын (1) ақ ырлы айырымдар қ атынасымен алмастырып (2) тең деудi мына тү рде жазамыз:
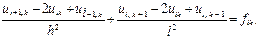 (4)
(4)
мұ ндағ ы 
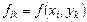
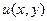 функциясының мә ндерiне қ атысты сызық тық алгебралық тең деулер жү йесiн бередi.
функциясының мә ндерiне қ атысты сызық тық алгебралық тең деулер жү йесiн бередi.
Дербес жағ дай. Егер G облысы тiк тө ртбұ рыш жә не 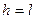 болса, онда (4) тең деулер былайша жазылады:
болса, онда (4) тең деулер былайша жазылады:
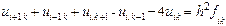

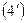
Егер 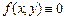 болғ анда (2) Лаплас тең деуі деп аталады.
болғ анда (2) Лаплас тең деуі деп аталады.
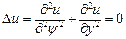 жә не сә йкес ақ ырлы-айырымдық тең деулер келесi тү рде жазылады:
жә не сә йкес ақ ырлы-айырымдық тең деулер келесi тү рде жазылады:
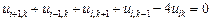
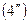
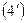 жә не
жә не 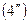 тең деулердi жазғ ан кезде келесi тү йiндер сұ лбасы қ олданылды:
тең деулердi жазғ ан кезде келесi тү йiндер сұ лбасы қ олданылды:
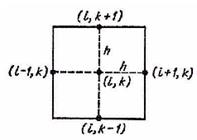
2-сурет
Дифференциалдық тең деудi айырымдық тең деумен алмастыру қ ателiгi, яғ ни Лаплас тең деуi ү шiн қ алдық мү ше 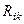 келесi тең сiздiкпен бағ аланады:
келесi тең сiздiкпен бағ аланады:
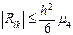
мұ ндағ ы
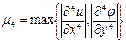
Айырымдық ә дiспен алынғ ан жуық таң шешiмнiң қ ателiгi келесi ү ш қ ателiктерден қ ұ ралады:
1. Дифференциалдық тең деудi айырымдық тең деумен ауыстырғ андағ ы қ ателiктен;
2. Шеттiк шарттарды жуық тау қ ателiгiнен;
3. Айырымдық тең деулер жү йесiн жуық тап шешу нә тижесiнде пайда болатын қ ателiктерден.
МЫСАЛ
Қ абырғ асы 1-ге тең, оқ шауланғ ан жазық шаршы пластинкадағ ы жылудың станционар ү лестірімі туралы есепті пластинканың шекарасында температура тұ рақ ты болғ ан жағ дайда қ арастырайық.
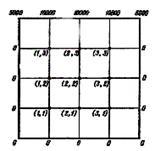
3-сурет
Температураның ү лестірімін беретін 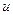 (
(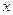 ,
, 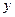 ) функциясы Лаплас тең деуінің шешімі болатыны белгілі:
) функциясы Лаплас тең деуінің шешімі болатыны белгілі:
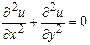
Берілген есеп ү шін шекаралық шарттар 3-суретте кө рсетілген.
Шешуі:
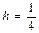 қ адаммен тор қ ұ рамыз, тоғ ыз ішкі тораптар аламыз. Осы тораптарда ақ ырлы-айырымдық тең деулер қ ұ рамыз.
қ адаммен тор қ ұ рамыз, тоғ ыз ішкі тораптар аламыз. Осы тораптарда ақ ырлы-айырымдық тең деулер қ ұ рамыз.
Шекаралық шарттардың симметриялылығ ын
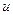 11=
11= 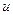 31,
31, 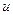 12=
12= 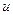 32,
32, 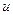 13=
13= 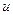 33 (1)
33 (1)
Бұ л 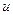 функциясының ішкі тораптардағ ы белгісіз мә ндерінің санын тоғ ыздан алтығ а дейін азайтады.
функциясының ішкі тораптардағ ы белгісіз мә ндерінің санын тоғ ыздан алтығ а дейін азайтады.
Осылайша (3, 1), (3, 2), (3, 3) тораптарда ақ ырлы-айырымдық тең деулерді жазудың қ ажеті жоқ. Қ алғ ан ішкі (1, 1), (2, 1), (1, 2), (2, 2), (1, 3), (2, 3) тораптарда сә йкес алты тең деуді аламыз:
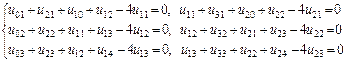
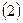
Бұ л тең деулер қ ұ рамына тағ ы функцияның шекаралық нү ктедегі 12 мә ні кіреді. Ол мә ндерді біз шекаралық шарттардан аламыз:
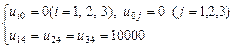 (3)
(3)
Қ алғ ан тораптарғ а шекаралық шарттар қ олданылмайды.
(2), (3) шарттарды ескере отырып, нақ ты тү рде келесі жү йені аламыз:
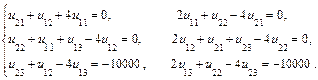
Бұ л жү йені Гаусс ә дісімен шешіп, алатынымыз:
