Пикар әдісі.

Бұ л y^/=f(x, y) (1) диффенерциалды тең деуді аналитикалық функция тү рінде жақ ындатылғ ан шешімін алуғ а мү мкіндік береді. Пикар ә дісі (1) тең деудің жалғ ыз шешімінің жә не табылу теоремасын дә лделдеуге байланысты пайда болады жә не мә ні бойынша сығ ылғ ан кө ріністің принципін қ олданудың бірі болып табылады. Бастапқ ы (2) шарты бар (1) тең деуінің шешімін табу теоремасының шартына сә йкес табу талап етілсін (1) тең деуінің екі жағ ын x₀-ден x-ке дейін интегралдаймыз:

y(x₀)=y₀ (5)

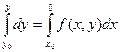
немесе

(5)

(5) интегралды тең деу шешімі дифференциалды тең деуді жә не бастапқ ы шартты қ анағ аттандырады.

Шынында да, x=x₀ кезінде аламыз:

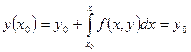
Сонымен (5) интегралдың тең деудің шешімі тізбекті жақ ындау ә дісін қ олдануғ а мү мкіндік береді. y=y₀ тең естіріп (5) тең деуінен бірінші жақ ындауды аламыз:

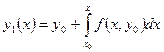
Оң жақ тағ ы интеграл тек x айнымалысынан тұ рады, бұ л интегралды тапқ аннан кейін y₁(x) жақ ындаудың аналитикалық ө рнегі x айнымалы функциясы сияқ ты алынады. Енді (5) тең деуінде у-те табылғ ан у₁(х) мә німен алмастырамыз жә не екінші жақ ындауды аламыз;

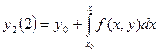
Жә не тағ ы сол сияқ ты.

Жалпы жағ дайда интеграциялық формула мынадай тү рде блады:

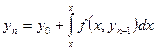
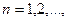(6)

(6) формуланың циклдық қ олдануы тө мендегі функция тізбегін береді:

Y₁(x), y₂(x), …, y_n(x) (7)

G-облысында f функциясы ү зіліссіз болғ андық тан, онда ол функция (х₀, у₀) нү ктесінен тұ ратын кейбір 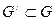облысында шектеулі болады, яғ ни

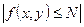(8)

Табылу теоремасы жағ дайында (6) тең деуіне қ ысылғ ан кө ріністер принципін қ олдана отырып (7) тізбегінің сә йкес келетін ( 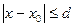сегментінде анық талғ ан φ кең істіктегі φ ү зіліссіз функциялар ρ (φ ₁, φ ₂)=max │ φ ₁(x)-φ ₂(x)│ метрикасы бойынша сә йкестік тү ріне айналады) кө рсету қ иын емес. Оның шегі интегралдық тең деу шешімі яғ ни (2) бастапқ ы шарты бар диффенерциалдық тең деу шешімі болып табылады. Бұ л (7) тезбегінің R-ші мү шесі анық талғ ан нақ талық дә режесі бар (1) тең деуінің нақ ты шешіміне жақ ындау болып табылады. R–ші жақ ындау қ ателігін бағ алау тө мендегі формуламен беріледі:

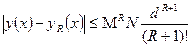(9)

Мұ нда М – Липшиц константасы (4) N- (8) тең сіздігіндегі f функциясының моділінің жоғ арғ ы шегі, ал 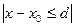аралығ ын анық тау ү шін d шамасы тө мендегі формула бойынша есептеледі.

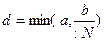. (10)

12.3. Біртіндеп жуық тау ә дісі

Коши есебін қ арастырайық. Біртіндеп жуық тау ә дісі бойынша 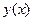шешімі 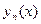функциясынын тізбектерінін шегі ретінде қ арастырылады. Жоғ арыда айтылғ ан шарттар қ анағ аттандырылсын деп ұ йғ арсақ, келесі рекуренттік формула бойынша 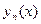табылады

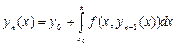(11)