Сандық интегралдау есебінің қойылуы.

Келесідей анық талғ ан интегралды есептегенде

,

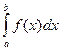мұ ндағ ы 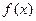функциясы 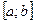кесіндісінде ү здіксіз, кейде белгілі Ньютон – Лейбниц формуласын қ олдануғ а болады:

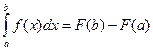(1)

мұ ндағ ы 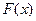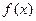функциясының алғ ашқ ыбейнелерінің бірі болады (яғ ни, 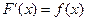). Бірақ, сирек жағ дайда, тә жірибе жү зінде алғ ашқ ыбейнені аналитикалық тү рде алғ анның ө зінде, анық талғ ан интегралдың сандық мә нін нақ ты соң ына дейін есептей алмаймыз. Оғ ан қ оса, кейде интеграл астындағ ы функция таблица немесе график тү рінде берілсе, онда интегралды не ү шін (6.18) формуласымен есептеу кең ауқ ымды практикалық қ олданыс алмайтыны тү сінікті болар еді.

Мұ ндай жағ дайда жуық тап (сандық) интегралдаудың ә ртү рлі тә сілдері қ олданылады.

Бір еселі интегралдарды жуық тап есептеуге қ олданылатын формулалар квадратуралық формулалар деп аталынады. Квадратуралық формулаларды қ ұ рудың қ арапайым ә дісі мынадай болады. Интеграл астындағ ы 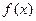функциясы 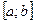кесіндісінде интерполяциялау кө пмү шелігімен алмастырылады. Мысалы, -Лагранж кө пмү шелігімен алмастырсақ, мынадай жуық тау тең дігі қ ұ рылады:

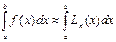, (2)

Мұ ндай ә діс ЭЕМ-де жең іл орындалатын алгоритмдерге ә келіп, нә тижені нақ ты алу мү мкіндігін береді. Бұ л жағ дайда, 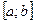кесіндісі 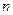бө лікке 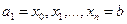нү ктелерімен бө лінеді, соның нә тижесінде кө пмү шелігі қ ұ рылады.

Алынғ ан нә тижені кө пмү шелігінің орнына қ оя отырып, біз

,

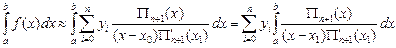мә нін аламыз.

Сонымен

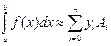, (3)

мұ ндағ ы

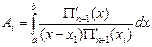, (4)

Осы табылғ ан формулалар нә тижесін біле отырып, мынаны байқ ауғ а болады:

1). 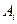коэффициенттері 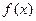функциясына тә уелді еместігі, себебі олар интерполяциялау тү йіндерін ескеріп қ ұ рылғ ан.

2). Егер 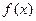, 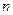-ші дә режелі полином болса, онда (2) формуласы нақ ты болады, себебі, бұ л жағ дайда .

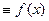Мұ ндағ ы x_к -интерполяцияның берiлген тү йіндер, А_к -функцияның тү рiне тә уелді емес тек тү йіндер таң дауына тә уелдi коэффициенттер, R -қ алдық мү ше немесе квадратуралық формуланың қ ателiгi.

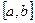интегралдау кесiндiсiн тең n бө лiкке бө лемiз:

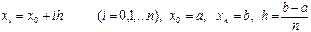
интеграл астындағ ы функцияны алынғ ан тораптарда есептеймiз.

Бiрдей қ ашық тық та жатқ ан тораптар ү шiн квадратуралық формулалар Ньютон-Котес формулалары деп аталады. Бұ ндай формулалардың қ арапайым тү рлерi тө менде келтiрiлген:

11.2 Трапеция формуласы.

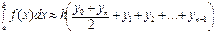(5)

мұ ндағ ы .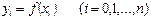

Қ алдық мү шесi келесi тү рде есептелiнедi:

11.3. Симпсон формуласы.

,

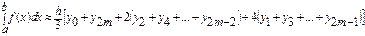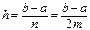(6)

Қ алдық мү шесi келесi тү рде есептелiнедi:

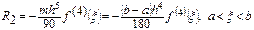
11.4. Ньютон формуласы.

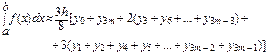(7)

мұ ндағ ы

.

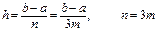Қ алдық мү ше келесi тү рде есептелiнедi:

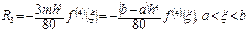
МЫСАЛ.

Келесі интегралды Симпсон формуласымен n=10 болғ анда есептеу керек:

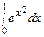
Шешуі.

Қ алдық мү шені бағ алау ү шін 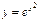функцияның тө ртінші ретті туындысын табайық.

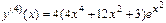
y⁽⁴⁾(x) туындысы [0, 1] кесіндісінде x=1 болғ анда ең ү лкен мә нді қ абылдайды. Сондық тан

| R₂ |£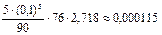

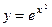функциясының мә ндер кестесін қ ұ райық.

i	x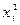
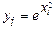
	0, 0	0, 00	1, 0000   2, 7188 3, 7188
	0, 1	0, 01		1, 0101
	0, 2	0, 04	1, 0408
	0, 3	0, 09		1, 0942
	0, 4	0, 16	1, 1735
	0, 5	0, 25		1, 2840
	0, 6	0, 36	1, 4333
	0, 7	0, 49		1, 6323
	0, 8	0, 64	1, 8965
	0, 9	0, 81		2, 2479
	1, 0	1, 00
Қ осынды	5, 5441	7, 2685

Симпсон формуласымен интегралды есептеп,

,

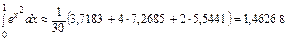нә тижені тө рт таң бағ а дейін дө ң гелектейміз: