Квадратуралық формулалардың дәлдігін бағалау туралы

Трапеция жә не Симпсон формулалары бойынша интегралдау ә дісінің қ ателігін бағ алау, тек интеграл астындағ ы функция аналитикалық тү рде берілгенде ғ ана мү мкін болады. Бұ л жағ дайдың ө зінде де, қ арастырылғ ан интегралдау ә дістерінің ә рқ айсысы ү шін жарамды, тә жірибе жү зінде кең інен қ олданылатын келесі ә дісті қ арастырамыз.

Ізделініп отырғ ан интеграл 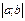кесіндісін n жә не 2n бө лікке бө лу арқ ылы 2 рет есептеледі (интегралдағ анда Симпсон формуласы бойынша n жұ п сан болу керек). Содан соң интегралдан алынғ ан мә н (оларды I_n жә не I_2n деп белгілейміз) салыстырылады жә не сә йкес бірінші ондық белгі дұ рыс деп саналады.

Симпсон ә дісінің қ ателігін бағ алау ү шін жай формула қ олданылады.

R_n, R_2n -Симпсон формуласы бойынша интегралдау қ ателіктері, сә йкесінше кесінді n жә не 2n бө лікке бө лінеді. (8.36) бағ алауды есептей отырып, мына тең дікті қ ұ руғ а болады:

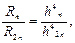(8)

Мұ ндағ ы, h_n жә не h_2n - кесіндінің бө лінгендегі ұ зындығ ы (нтегралдау қ адамы) 1-ші жә не 2- ші жағ дайда.

Бізге белгілі h_2n =h_n /2 (6.38) формуладан аламыз:

R_n=16R_2n (9)

Егер I-интегралдық шын мә н болса, онда I=I_n+R_n жә не I=I_2n +R_2n бұ дан I+16R_2n=I_2n+R_2n, яғ ни:

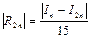(10)

(6.40) формула Симпсон ә дісінің қ ателігін тә жірибелі бағ алауда қ олайлы, бірақ екі рет есептеуді қ ажет етеді.

(6.33) жә не (6.36) бағ алау формулаларынан трапеция жә не Симпсон ә дістері бойынша интегралдау қ ателігі интегралдау қ адамының азаюымен бірге азаюы байқ алады. (ә сіресе бұ л (6.39) Симпсон формуласына тә н). Осының негізінде шешім қ абылдайық, бө лінген кесіндінің саны біртіндеп ө скенде біз интегралдың мә нін аламыз, бұ ның бә рі шындық қ а жуық тайды. Бірақ бұ ның шешімі теориялық мә нге тура келеді. Тә жірибе жү зінде есептесек бө лінген кесіндінің саны біртіндеп екі еселенгенде қ ателіктің салмағ ы жуық тап алынады. Бұ ның мә ні ә рбір моментке дейін интегралдық шешімнің жеткен нү ктесіне шектеу қ ояды (нақ тылай қ арасақ кө рсетілген қ атенің интегралдық шешіміне ә сері кө рсетілген).

Бақ ылау сұ рақ тары:

1. Сандық дифференциалдау есебінің ерекшелігі неде?

2. Қ адамды тізбектей азайту арқ ылы интегралдауда жіберілетін

қ ателікті шексіз азайту мү мкін бе?

Дә ріс. Қ арапайым дифференциалдық тең деулердi шешу. Коши есебінің бір жә не кө п қ адамды ә дістері. Орнық тылық. Жинақ тылық. Берік жү йелерді интегралдау.

12.1. Қ арапайым дифференциалдық тең деулерді сандық шешу