Случайной величины

Пусть (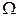, F, P) – произвольное вероятностное пространство.

Определение. Числовая функция 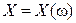элементарного события 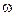с областью определения 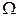называется случайной величиной, если :

.

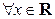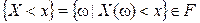Возможные значения x функции 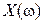называются реализациями случайной величины .

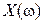Комментарий. Смысл этого определения состоит в следующем. Поскольку не любое подмножество 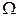является событием, и все события составляют s-алгебру подмножеств F, то естественно рассматривать такие функции 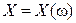, для которых имеет смысл говорить о вероятностях попадания 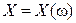в достаточно простые числовые множества, в частности, множества 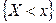. Свойство 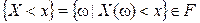гарантирует, что при любом x неравенство 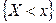есть событие, а значит, имеет смысл говорить о его вероятности.

Замечание. Если вероятностное пространство (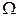, F, P) – конечно, то случайной величиной называют любую числовую функцию 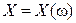от элементарного события .

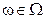Будем обозначать случайные величины прописными (большими) буквами латинского алфавита: X, Y, Z, …; а их возможные значения (реализации) – соответствующими строчными (малыми) буквами x, y, z, …

Пример 2.1.1. Опыт – бросание игральной кости. Случайная величина X – число выпавших очков. Множество возможных значений (реализаций) является конечным: {1, 2, 3, 4, 5, 6}.

Пример 2.1.2. Опыт – с помощью точного прибора дважды измеряется емкость конденсатора. Случайная величина X – разность между результатами первого и второго измерений. Множество возможных значений (реализаций) – все точки числовой оси.

Определение. Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всех возможных событий, связанных со случайной величиной.

Если случайная величина X имеет данный закон распределения, то говорят, что случайная величина распределена по этому закону (подчинена этому закону распределения). Наиболее общей формой закона распределения пригодной для любых случайных величин является функция распределения.

Определение. Функция 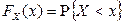, определенная 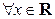, называется функцией распределения случайной величины Х.

С помощью функции распределения можно вычислять вероятности попадания случайной величины Х в различные промежутки вида 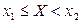, , 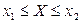, , 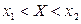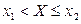а также вероятность события :

, ,

, ,

.

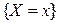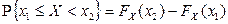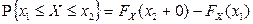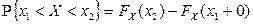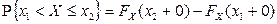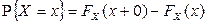Функция обладает следующими свойствами:

1. ;

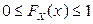
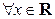2. не убывает;

3. непрерывна слева;

4. , .

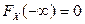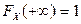Пример 2.1.3. Известно, что 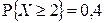. Найти .

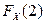Решение. По определению функции распределения . Следовательно, 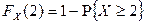. Поэтому .

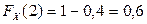Ответ: 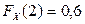.