Функция распределения

Для непрерывной случайной величины закон распределения нужно задавать по-другому, чем в случае дискретной случайной величины.

Рассмотрим наиболее общий подход к формулировке закона распределения и введем наиболее общую и универсальную характеристику случайных величин – функцию распределения, которая вводится соотношением

.

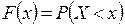
Таким образом – это вероятность того, что случайная величина 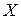примет значение меньшее, чем .

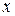Геометрически это означает следующее: 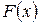– вероятность того, что случайная величина 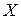примет значение, которое изображается точкой на числовой прямой, расположенной слева от точки .

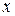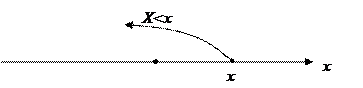Теперь можно дать такое определение непрерывной случайной величины.

Случайная величина называется непрерывной, если ее функция распределения 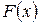является непрерывно дифференцируемой.

Функцию распределения называют также интегральной функцией, или интегральным законом распределения случайной величины .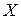

Если дана функция распределения 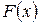, то нетрудно вычислить и вероятность попадания величины в интервал 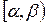, т.е. .

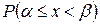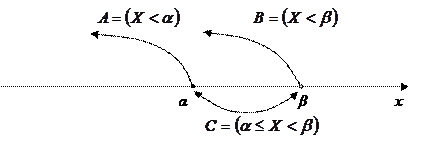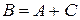, но .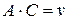

Применима формула сложения вероятностей

,

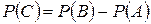но

,

,

.

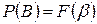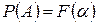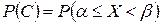Значит,

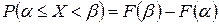. (1)

Отметим еще свойства функции распределения.

1с. 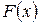неубывающая функция. Действительно, это следует из (1), т.к. 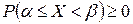, то из 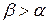следует .

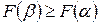2с. Если все возможные значения случайной величины 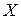принадлежат интервалу 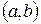, то для ее функции распределения

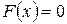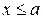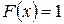при ,

при .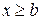

Если же все возможные значения случайной величины х принадлежат бесконечному интервалу 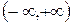, то

.

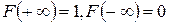Эти свойства позволяют говорить о графике функции распределения – это график неубывающей функции, значения которой начинаются от нуля и

доходят до 1, причем в отдельных точках могут быть разрывы 1 ^го ряда (скачки).

Функция распределения 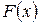для дискретной случайной величины 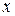, которая может принимать значения 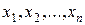с соответствующими вероятностями: 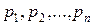, имеет вид:

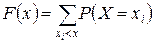. (2)

(это означает, что суммируются вероятности тех значений, которые меньше х.)

Пример. Закон распределения дискретной случайной величины задан следующей таблицей:

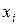
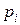
	0, 2	0, 4	0, 3	0, 1

Найти функцию распределения случайной величины.

Решение. Для построения функции распределения воспользуемся формулой (2).

1) При .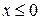

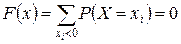2) При .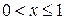

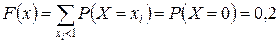3) 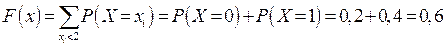При .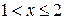

1)

4) При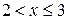

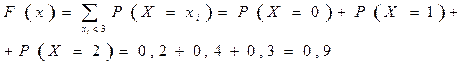
5) 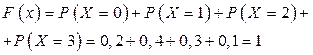При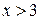

.

Будем неограниченно уменьшать интервал 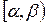, полагая 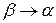. В пределе, очевидно, получим вероятность того, что величина примет одно заданное определенное значение.

.

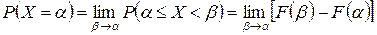Если 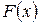– непрерывна, то этот предел равен нулю, т.е. 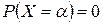. Таким образом, вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Заметим, что равенство нулю вероятности отдельно взятого значения случайной величины не означает, что эта величина не может появиться. Из того, что 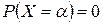следует только, что при неограниченном повторении опыта данное событие должно появиться однократно, или крайне редко.

Например, изготовление эталонов.

Исходя из сказанного выше, должны выполняться равенства:

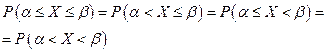
и

.
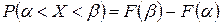