Локальная и интегральная теоремы Муавра-Лапласа

Для вычисления вероятности 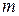успехов в 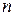испытаниях по схеме Бернулли мы получили формулу

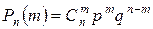
и отметили трудоемкость ее применения при больших .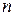

Приняв некоторые допущения при больших 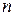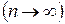, а именно 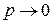, , 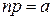получили формулу Пуассона

.

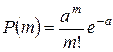И отметили, что ее обычно используют пр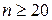и и 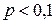. Такое приближение называют асимптотикой Пуассона.

Покажем как можно вычислять подобные вероятности, основываясь на формулах нормального распределения. Говорят в этом случае об асимптоте Муавра-Лапласа.

Пусть число испытаний 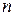по схеме Бернулли велико, тогда для вероятности 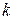успехов справедлива следующая приближенная формула:

,

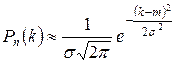где , .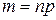

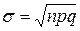Ранее мы ввели нормированную (стандартную) функцию плотности нормального распределения

.

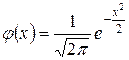Пользуясь этой функцией, нетрудно получить такую формулу:

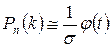, (1)

где , , .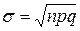

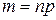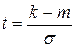Формулу (1) называют локальной формулой Муавра-Лапласа.

Используя формулу (1), можно записать выражение для верности того, что число успехов заключено между числам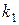и и .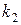

,

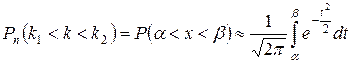где , .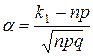

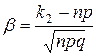Выражение справа можно записать, используя функцию Лапласа и получим формулу, называемую интегральной формулой Лапласа.

.

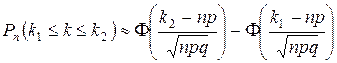Обычно формулы Муавра-Лапласа применяются в качестве приближенных формул пр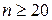и и .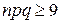

Пример 1. Вероятность попадания в цель при одном выстреле равна 0, 8. Определить вероятность того, что при 400 выстрелах произойдет ровно 300 попаданий.

Решение. ,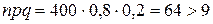

.

,

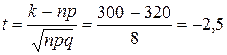находим по таблицам .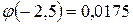

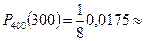0, 0022.

Пример 2. Правильную игральную кость бросают 600 раз. найти вероятность того, что «двойка» выпадает от 90 до 120 раз.

Решение.

,

,

.

.
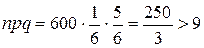
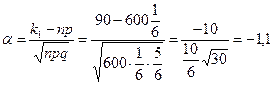
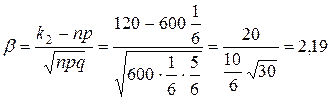
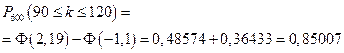