Биномиальное распределение. Говорят, что случайная величина, выражающая число успехов в схеме испытаний Бернулли имеет биномиальное распределение

Говорят, что случайная величина, выражающая число успехов в схеме испытаний Бернулли имеет биномиальное распределение

.

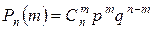Для биномиального распределения можно вывести числовые характеристики.

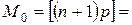целое число от .

,

,

.

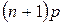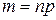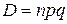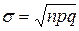Продолжим рассмотрение предыдущего примера и получим ряд распределения для 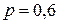, а также числовые характеристики.

;

;

;

.

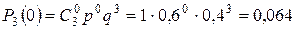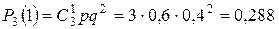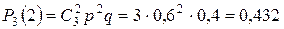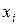
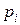
	0, 064	0, 288	0, 432	0, 216

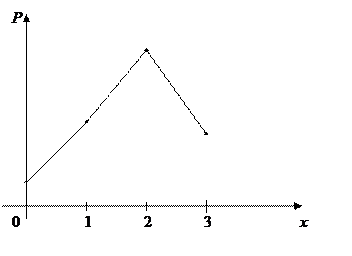
Числовые характеристики

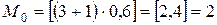– это значит случайная

величина соответствует наибольшей вероятности;

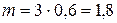– среднее число успехов;

;

.

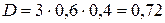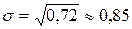Число 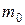, которому при заданном 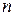соответствует максимальная биномиальная вероятность 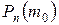называется наивероятнейшим числом появления события 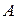. При заданных 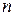и 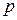это число определяется неравенствами

.

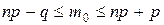Если число 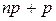не является целым, то 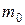равно целой части этого числа

.

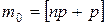Если же 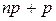– целое число, то 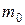имеет два значения

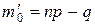и .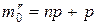

Пример. Доля изделий высшего сорта на данном предприятии составляет 30%. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий.

Решение. По условию 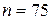, , 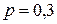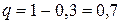. Составляем двойное неравенство:

,

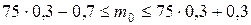
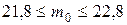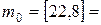22.

Замечания:

1. Если требуется вычислить вероятность того, что число успехов 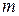при 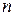испытаниях заключено между натуральными числам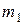и и 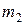, то, воспользовавшись независимостью испытаний и теоремой сложения вероятностей, получим следующую формулу

.

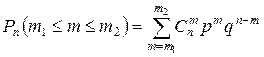2. Вероятность получения хотя бы одного успеха при 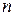испытаниях можно найти, используя противоположное событие:

.

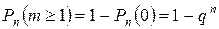Пример. Симметричную монету бросают шесть раз. Определить вероятность выпадения цифры:

а) ровно 4 раза

.

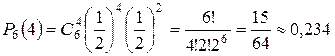б) не более 3 ^х раз

.

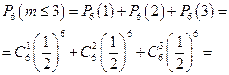
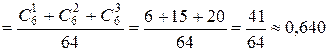в) хотя бы один раз

.

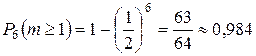Когда число независимых испытаний 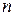велико, вычисление 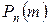по формуле Бернулли затруднительно, т.к. требует вычисления факториалов больших чисел. В дальнейшем мы получим асимптотические формулы, используемые при больших .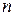