Нормальное распределение. Нормальным Гауссовым называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Нормальным Гауссовым называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

.

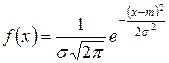Видим, что нормальное распределение определяется двумя параметрами т и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение.

Вычислим математическое ожидание.

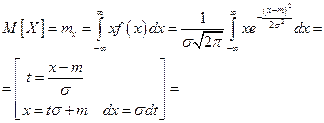
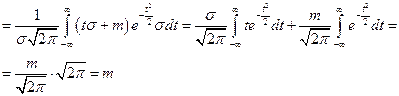Итак, 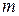имеет смысл математического ожидания.

Найдем теперь дисперсию.

, ,

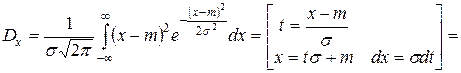
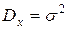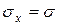т.е. 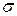– имеет смысл с.к.о.

Вычисляя моменты, найдем

,

.

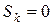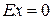Если параметры 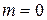, , 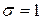то такое распределение называется нормированным, его плотность вероятности определяется выражением

.

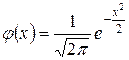Она табулирована.

Напомним, что

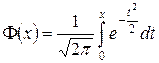
называется функцией Лапласа. Она табулирована. Ее основные свойства:

1) 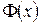– монотонно возрастающая.

2) .

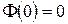3) 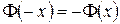, т.е. нечетная

4) .

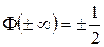Вычислим вероятность попадания случайной величины, распределенной по нормальному закону в интервал :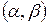

.

.

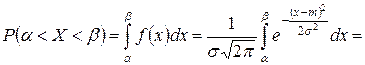
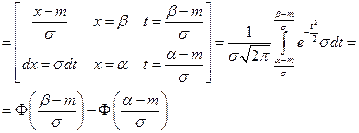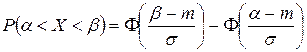Пример. По автостраде шириной 20м ведется стрельба по направлению ей перпендикулярном. Прицеливание по середине. Известно, что 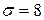м. имеется систематическая ошибка в направлении стрельбы – недолет 3м. Найти вероятность попадания в автостраду при одном выстреле.

Нас интересует 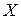– случайная величина – абсцисса попадания снаряда. Эта случайная величина распределена по нормальному закону с параметрами 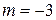, 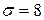. Таким образом, попадание в автостраду – это попадание случайной величины в интервал .

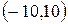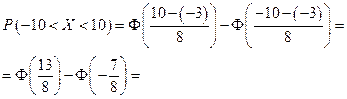
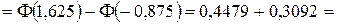0, 7571.

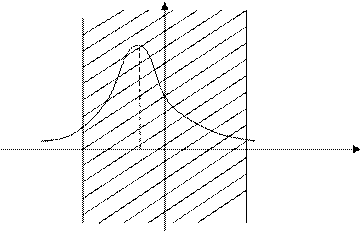
Рассмотрим интервал, симметричный относительно математического ожидания 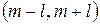и найдем вероятность в этот интервал.

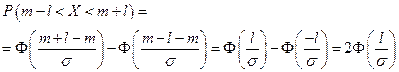
или

.

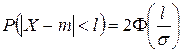Если положить 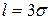, то получим

.

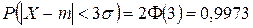Отсюда следует, что почти все значения (99, 73%) нормально распределенной случайной величины попадают в интервал 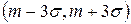. Этот факт называют «правилом трех сигм». Интервал 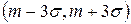называется зоной практического рассеивания.

Пример. Технологической операцией предусмотрено изготовление изделий с симметричным относительно расчетного значения полем допуска шириной 0, 3. определить, сколько будет получаться в среднем точных изделий с симметричным полем допуска шириной 0, 05.

Решение.

,

.

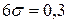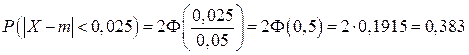
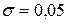, т.е. 38, 3%.