Ателіктердің классификациясы.

Математикалық есептерде кездесетін қ ателіктерді негізінен бес топқ а бө леді:

1) Есеп қ ателіктері, басқ аша айтқ анда, математикалық есептің берілуімен байланысты қ ателіктер. Қ андайда бір қ ұ былыстың математикалық сипаттамасы нағ ыз қ ұ былыспен ү немі дә л келе бермейді: ә детте олар тек қ ана салыстырмалы тү рде қ андайда болмасын идеал модель бейнесінде беріледі. Табиғ аттың қ андайда бір қ ұ былысын зерттеу барысында біз есепті жең ілдету мақ сатында белгілі бір шарттарды қ абылдауғ а мә жбү р боламыз бұ л ә рекер бірқ атар қ ателіктердің тууына себеп болады.

Ә діс қ ателігі. Кей жағ дайда есепті тура қ ойылымында шешу қ иын немесе тіпті мү мкін емес. Бұ л жағ дайда берілген есепті нә тижесі жуық талғ ан тү рде берілген есеп нә тижесіне тең болатын басқ а есеппен ауыстыруғ а тура келеді. Осы кезде ә рине қ ателік пайда болады, мұ ндай қ ателік тү рін ә діс қ ателігі деп атайды. Мысалы, аналитикалық тү рде берілген есепті сандық есеппен алмастыру ә діс қ ателігіне жатады.

2) Қ алдық қ ателіктері, басқ аша айтқ анда, математикалық анализдегі шексіз процесстермен байланысты қ ателіктер. Математикалық формулаларда қ олданылатын функциялар шексіз тізбектер немесе қ атарлар тү рінде берілуі сирек емес. (мысалы, 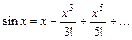). Тіптен кө птеген математикалық тең деу-лерді – шектері (lim) осы тең деулердің шешімдері болып табылатын шексіз процестерді сипаттау арқ ылы ғ ана шешуге болады. Шексіз процесс, жалпы айтқ анда, белгілі бір қ адамнан кейін (шектеулі қ адамда) бітпейтіндіктен, біз осы тізбектің қ андайда бір мү шесінде тең деудің жуық талғ ан шешімін алдық деп тұ жырымдап тоқ тауғ а мә жбү р боламыз. Процесті бұ лай тоқ тату ә рине қ ателікті тудырмай қ ой-майды.

3) Дө ң гелектеу қ ателіктері. Санау жү йелерімен байланысты қ ателіктер. Тіптен ондық санау жү йелерінде рационал сандарды ө рнектеу барысында, ү тірден кейін оң жақ та орналасатын цифрлар саны шексіз болуы мү мкін. Мысалы, 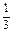рационал сан, ондық бө лшек тү ріне келтіргенде 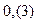периодты санына тең болады. 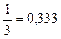десек, нә тижесінде 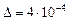қ ателігін аламыз. Иррационал сандарды да осы тү рде дө ң гелектеуге тура келеді.

4) Ә рекет қ ателіктері. Жуық талғ ан сандарғ а қ олданылатын ә рекеттермен байланысты қ ателіктерді айтады. Жуық талғ ан сандарғ а қ андайда бір ә рекеттер қ олдана отырып, біз нә тижені де жуық тап табамыз. Бұ л жағ дайда ә рекет қ ателіктері тү зетілмейтін қ ателіктер болып табылады.

5) Бастапқ ы қ ателіктер. Математикалық формулаларда мә ні тек қ ана жуық тап анық талатын сандық параметрлердің болуымен байланысты қ ателіктер. Мысалы, барлық физикалық тұ рақ тылар осындай сандық параметрлер қ атарына жатады.

Бақ ылау сұ рақ тары:

1. Есептеу эксперименті дегеніміз не?
2. Есептерді сандық ә дістерді қ олданып шешуде қ андай талаптар орындалуы керек?
3. ЭЕМ-де есептерді шешу барысында қ ателіктердің қ андай тү рлері болуы мү мкін?
4. Айталық х -кейбір шаманың дә л мә ні, ал а жуық мә ні болатын болсын. Сонда 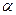жуық тауының абсолюттік қ ателігі дегеніміз не?
5. Қ андай да 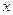-шамасының а -жуық тауының салыстырмалы қ ателігі 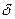-саны дегеніміз не?