Алгебралық және трансцендент теңдеулерді сандық шешу. Графиктік әдіс.

Айталық

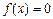(1)

тең деуінің тү бірлерін анық тау керек, мұ нда 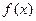- қ андай да бір ақ ырлы немесе ақ ырсыз 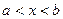аралығ ында анық талғ ан жә не ү зіліссіз функция.

Анық тама 1. 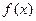фунқ циясын нө лге айналдыратын, қ андай да бір x мә ні (1) тең деудің тү бірі деп аталады.

Анық тама 2. f(x) функциясының анық талу 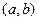облысына тиісті (1) тең деудің тек бір ғ ана тү бірі жататын 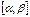аралық тарын анық тау тең деудің тү бірлерін жекешелеу деп аталады.

Анық тама 3. Тү бірлерді жекешелеу кезінде анық талғ ан аралық тағ ы тең деудің тү бірі ү шін қ абылданғ ан бастапқ ы жуық тауды e дә лдіктің дә режесіне дейін жеткізуді тү бірді дә лдеу деп атайды.

(1) тең деудің тек бір тү бірі жатқ ан кіші аралық ты анық тау ү шін математикалық талдау курсынан келесі теорема колданылады.

Теорема. Егер 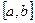аралығ ында анық талғ ан, ә рі ү зіліссіз 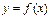фунқ циясы 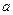жә не 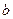нү ктелерінде қ арама - қ арсы таң балы мә ндерді қ абылдаса, яғ ни

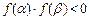(2)

тең сіздігі орындалса, онда осы аралық та (1) тең деуінің кем дегенде бір тү бірі болады.

Ал егер осындай 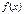функциясының туындысы бар болып жә не ол осы 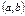аралығ ында таң басын ө згертпесе, онда 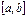аралығ ында (1) тең деудің жалғ ыз тү бірі болады.

(1)-ші тең деудің нақ ты тү бірлері 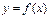қ айсысының Ох осімен қ иылысқ ан нү ктелерінің абсциссалары болғ андық тан тү бірлерді жекешелеуді графиктік ә діспен анық тасақ болады.

Графиктік ә дісінің алгоритмі:

1) (1) тең деуді ө зімен пара-пар тең деумен алмастыруғ а болады

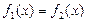
мұ ндағ ы 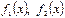– функциялары 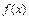функциясына қ арағ ан-да қ арапайым фунқ циялар болуы тиіс;

2) 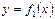жә не 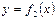функцияларының графиктерін саламыз;

3) осы графиктердің қ иылысу нү ктелерінің абсциссаларын анық таймыз;

4) Егер табылғ ан абсциссалар мә ндері (2) тең сіздікті қ анағ аттандырса, онда осы графиктердің қ иылысу нү ктелерінің абсциссалары берілген тең деудің ізделінді тү бірлері болып табылады. Егер (2) тең сіздік орындалмаса, онда 3-ші пунктке ораламыз.