Матрица ұғымы және түрлері.

Анық тама. Сандардан немесе қ андай да бір басқ а элементтерден тұ ратын тікбұ рышты кестені матрица деп атайды да, оны екі жағ ынан жақ ша немесе қ ос тү зу сызық тармен шектеп жазады.

Мысалғ а, матрицалар тө мендегідей:

, ,

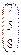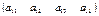
тү рлерінде жазылады.

Анық тауыштардағ ы сияқ ты матрицалар да жатық жолдардан жә не тік бағ аналардан тұ рады. Сондық тан да матрицаның элементтерінің орындарын жатық жол жә не тік бағ ана нө мірлері арқ ылы ажырататын боламыз. Ал матрицаның анық тауыштан айырмашылығ ы – анық тауыш сияқ ты бір санғ а тең болмайтындығ ында.

Матрицаның қ ысқ аша бір ғ ана ә ріппен т.с.с.) белгілеп жазуғ а болады, ә рине бір ә ріппен жазылғ ан матрицаны кестие деп тү сінуіміз керек.

Егер матрицаның элементтерін 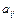арқ ылы белгілейтін болсақ, онда жалпы тү рде 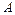матрицасы деп мына

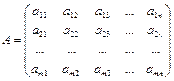
жатық жолдан жә не 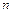тік бағ анадан тұ ратын тікбұ рышты кестені ұ ғ амыз.

Анық тауыш сияқ ты матрицаның элементтерін де екі индекс арқ ылы жазғ ан қ олайлы. Оның біріншісі – жатық жол нө мірін, ал екіншісі – тік бағ ана нө мірін кө рсететін болады. Матрицада жалпы мө лшер ұ ғ ымын ғ ана пайдалануғ а болады. Тек 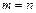болғ ан жағ дайда ғ ана матрица реті айтылады.

Егер матрицаның мө лшері 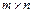, яғ ни 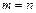болса, она ондай матрицаны квадрат матрица деп атайды.

Матрицаның жатық жолдары мен тік бағ аналарының орындарын ауыстыруғ а болады. Осындай ә рекет нә тижесінде шық қ ан матрицаны транспозицияланғ ан матрица деп атайды да, оны 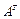тү рінде белгілейді.

Мысалы, берілген матрица

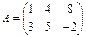
болса, онда транспозицияланғ ан матрица

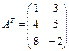
болады.

Егер берілген матрица 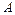ө зінің транспозицияланғ ан матрицасымен дә л келетін болса, яғ ни

,

Онда мұ ндай матрица симметриялы матрица деп аталады. Матрицаның бұ л шартын

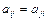
тү рінде жазуғ а болады.

Матрицалардың барлық тү рлерінің ішінде тек квадрат матрианың ғ ана анық тауышы болады жә не оны не , не 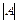тү рінде жазады. Егер 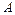квадрат матриа болса, онда

,

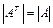Демек анық тауыштың шамасы оны транспозициялаудан ө згермейді.